Fraud Dectection Using Keras
Keras 를 활용해서, kaggle 의 유명한 예제인 Fraud_Detection 을 해보자.
참고주소 Medium
Venelin Valkov github original
import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
from scipy import stats
## local PC 에서, gpu 메모리를 다른 프로세서가 선점하고 있을때, 다시 설정해주는 코드임
import tensorflow as tf
from keras.backend import tensorflow_backend as K
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
K.set_session(tf.Session(config=config))
Using TensorFlow backend.
import seaborn as sns
from pylab import rcParams
from sklearn.model_selection import train_test_split
from keras.models import Model, load_model
from keras.layers import Input, Dense
from keras.callbacks import ModelCheckpoint, TensorBoard
from keras import regularizers
%matplotlib inline
sns.set(style='whitegrid', palette='muted', font_scale=1.5)
rcParams['figure.figsize'] = 14, 8
RANDOM_SEED = 42
LABELS = ["Normal", "Fraud"]
df = pd.read_csv("D:/★2020_ML_DL_Project/Alchemy/dataset/creditcard.csv")
df.shape
(284807, 31)
null 값 체크
df.columns.isnull().any()
False
df.isnull().values.any()
False
count_classes = pd.value_counts(df['Class'], sort = True)
count_classes.plot(kind = 'bar', rot=0)
plt.title("Transaction class distribution")
plt.xticks(range(2), LABELS)
plt.xlabel("Class")
plt.ylabel("Frequency");
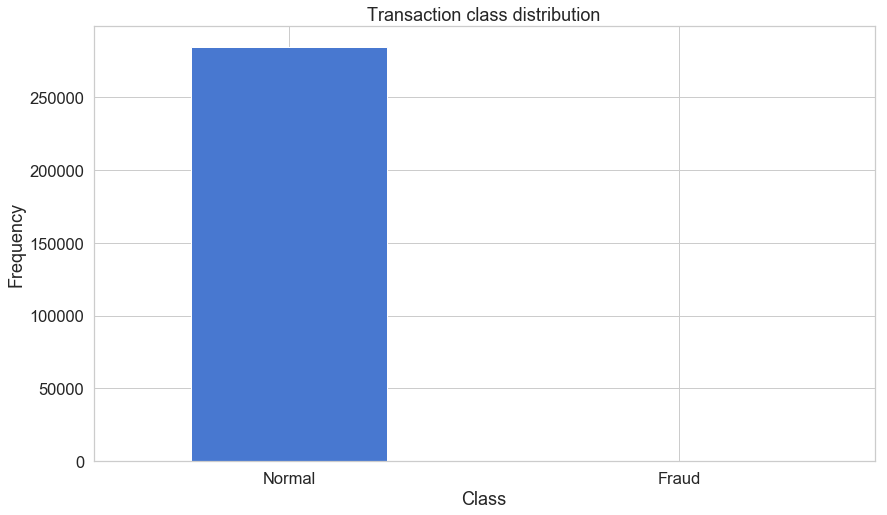
전형적인 불균형 imbalanced data 양상을 보이고 있다. 99.9 % vs 0.1 % 임
print(df.Class.value_counts())
print((df.Class.value_counts()/df.Class.count())*100)
0 284315
1 492
Name: Class, dtype: int64
0 99.827251
1 0.172749
Name: Class, dtype: float64
frauds = df[df.Class == 1]
normal = df[df.Class == 0]
pd.concat([frauds.Amount.describe(),normal.Amount.describe()],axis=1,names=['fraud','normal'])
| Amount | Amount | |
|---|---|---|
| count | 492.000000 | 284315.000000 |
| mean | 122.211321 | 88.291022 |
| std | 256.683288 | 250.105092 |
| min | 0.000000 | 0.000000 |
| 25% | 1.000000 | 5.650000 |
| 50% | 9.250000 | 22.000000 |
| 75% | 105.890000 | 77.050000 |
| max | 2125.870000 | 25691.160000 |
데이터는 게다가, 모두 float64 (숫자형데이터)이며, 그중 특이하게 Time 데이터가 있다.
df.dtypes
Time float64
V1 float64
V2 float64
V3 float64
V4 float64
V5 float64
V6 float64
V7 float64
V8 float64
V9 float64
V10 float64
V11 float64
V12 float64
V13 float64
V14 float64
V15 float64
V16 float64
V17 float64
V18 float64
V19 float64
V20 float64
V21 float64
V22 float64
V23 float64
V24 float64
V25 float64
V26 float64
V27 float64
V28 float64
Amount float64
Class int64
dtype: object
df.Time.tail()
284802 172786.0
284803 172787.0
284804 172788.0
284805 172788.0
284806 172792.0
Name: Time, dtype: float64
데이터가 특이해서 찾아보니, 변수 설명이 있었다.
- Time : Number of seconds elapsed between this transaction and the first transaction in the dataset
이 트랜잭션과 데이터 세트의 첫 번째 트랜잭션 사이에 경과된 시간(초)
- (v1-v28) : may be result of a PCA Dimensionality reduction to protect user identities and sensitive features(v1-v28)
f, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
f.suptitle('Amount per transaction by class')
bins = 50
ax1.hist(frauds.Amount, bins = bins)
ax1.set_title('Fraud')
ax2.hist(normal.Amount, bins = bins)
ax2.set_title('Normal')
plt.xlabel('Amount ($)')
plt.ylabel('Number of Transactions')
plt.xlim((0, 20000))
plt.yscale('log')
plt.show();
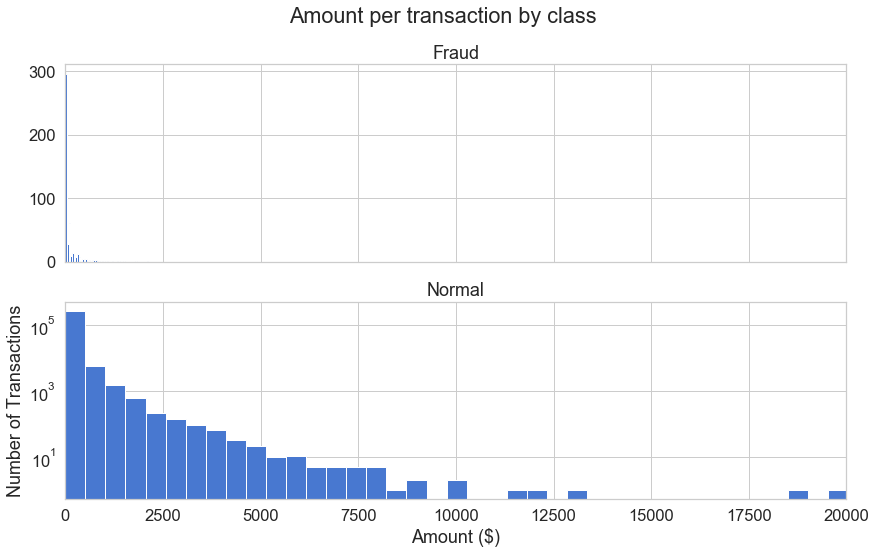
Fraud 그룹이 발생한 금액대는 대부분 1000 미만의 금액대인것이 보인다.
ax=frauds.Amount.plot(kind='kde')
ax.set_xlim(0,1000)
(0, 1000)
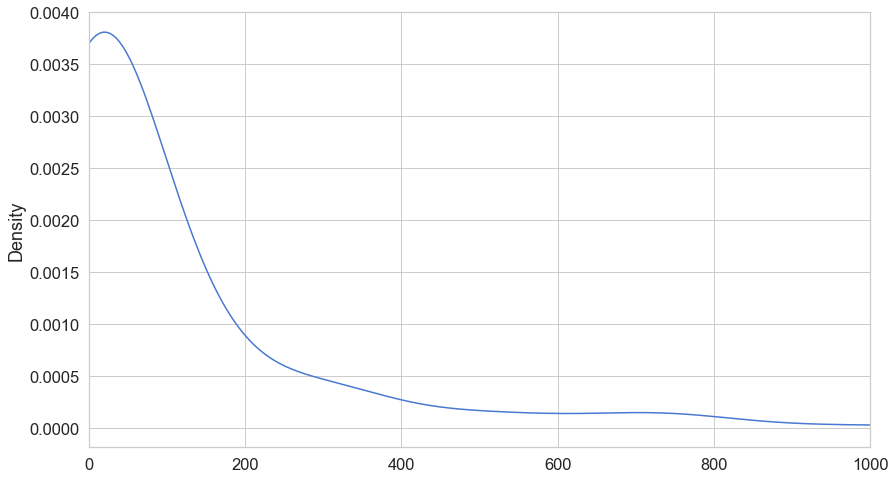
시각화하니, Fraud 건들은 주로 1000건 이하, 특히 400건 이하에서 이루어지고 있음을 알 수 있다.
f1 = lambda x : "{:.4f}".format(x)
frauds.Amount.describe().apply(f1)
count 492.0000
mean 122.2113
std 256.6833
min 0.0000
25% 1.0000
50% 9.2500
75% 105.8900
max 2125.8700
Name: Amount, dtype: object
frauds.Amount.quantile(0.98)
938.0828000000004
normal.Amount.describe().apply(f1)
count 284315.0000
mean 88.2910
std 250.1051
min 0.0000
25% 5.6500
50% 22.0000
75% 77.0500
max 25691.1600
Name: Amount, dtype: object
print(normal.Amount.quantile(0.99)) ## 상위 1% 구간은 1016.966 이다
print(normal.Amount.quantile(0.999))
1016.9663999999966
3000.0
normal 그룹 vs Fraud 그룹 둘다 std 는 250 가량인데, 평균과 중위값이 차이가 있다.
fraud : mean/중위값 = 122 /9.25
normal : mean/중위값 = 88 / 22
둘다 중위값에 비해, 평균값이 크다 -> 분포가 왼쪽 Skewed 가 있다. 오른쪽 꼬리 모양 fraud 가 좀더 편향값이 심하다. 이를 hist 가 아닌 kde 로 재확인해보면,
plt.figure(figsize=(7,5))
df.groupby(by=['Class']).Amount.plot(kind='kde',xlim=(0,2000))
plt.legend()
<matplotlib.legend.Legend at 0x1b0e876f860>
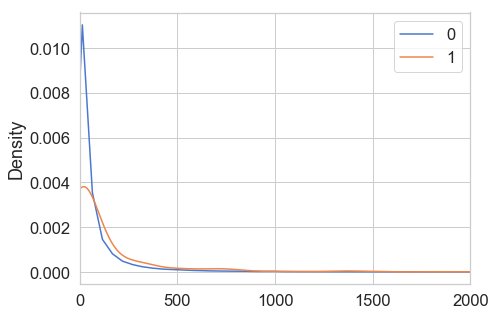
Amount 가 1500 이상이 차지하는 비율을 확인해보면, 1350 row 임. 이중 Fraud 갯수는 3 개 이므로, 이상치로 판단 제거한다.
print(df.loc[df.Amount >= 1500,:].shape)
print(df.loc[df.Amount >= 1500,'Class'].value_counts())
print(df.loc[df.Amount >= 1500,'Class'].value_counts().iloc[1]/(df.loc[df.Amount >= 1500,:].shape[0])*100)
(1350, 31)
0 1347
1 3
Name: Class, dtype: int64
0.2222222222222222
df01 = df.loc[df.Amount < 1500,:]
df -> df01 로 이상치 제거한 상태에서, 다시 시작
from sklearn.preprocessing import StandardScaler
data = df01.drop(['Time'], axis=1)
data['Amount'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1, 1))
data['Amount'].head()
0 0.473716
1 -0.482156
2 1.963764
3 0.303789
4 -0.044327
Name: Amount, dtype: float64
우리의 목적은 이상거래 탐지인데 여기선, 모델을 정상거래만으로 이루어진걸로 train 시키고, 테스트 세트(20%)에 올바른 클래스를 잡아두면 우리 모델의 성능을 평가할 수 있다.
X_train, X_test = train_test_split(data, test_size=0.2, random_state=RANDOM_SEED)
X_train = X_train[X_train.Class == 0]
X_train = X_train.drop(['Class'], axis=1)
## 모두 정상거래인 data
print("X_train.shape",X_train.shape)
X_train.shape (226381, 29)
type(X_train)
pandas.core.frame.DataFrame
y_test = X_test['Class']
X_test = X_test.drop(['Class'], axis=1)
## 20% 의 테스트셋에는, 비정상 거래가 들어있다. 대략 0.2 % 가량의 불균형을 보이고 있다
print(y_test.value_counts())
print(y_test.value_counts()/y_test.count()*100)
0 56587
1 105
Name: Class, dtype: int64
0 99.814789
1 0.185211
Name: Class, dtype: float64
X_train = X_train.values ## array type 으로 바꾼다. keras DL 에서는 Dataframe을 사용할수 없기때문
X_test = X_test.values
## 0번째 행의 값을 보면 알수 있듯이 PCA로 일단, 어느정도 scaling 이 되어있다고 보고, 원저자는 따로 scale 변환을 안한것 같다.
X_train[0]
array([ 1.0497864 , 0.13341122, 1.48434448, 2.74270707, -0.83528583,
0.16557882, -0.504702 , 0.15437609, 0.10466168, 0.47498457,
-0.95249838, 0.17203493, 0.0535732 , -0.40718252, -0.29895828,
0.62560213, -0.41437543, -0.19339594, -0.8548623 , -0.08279022,
-0.06251716, -0.11457316, 0.01110139, 0.3892984 , 0.28355026,
-0.04787002, 0.03551502, 0.04264667, -0.24222819])
print(type(X_train),X_train.shape)
<class 'numpy.ndarray'> (226381, 29)
Keras 모델 만들기 - Autoencoder 모델은 여기선, fully connected layers 로 14-7-7-14 를 이용한다.
함수형 API 로 네트워크 층 만들기
================Start================
input_dim = X_train.shape[1]
## input_layer
input_layer = Input(shape=(input_dim, ))
## Dense_layer first Encoder - 14
encoding_dim = 14
encoder = Dense(encoding_dim, activation="tanh", activity_regularizer=regularizers.l1(10e-5))(input_layer)
## Dense_layer Second Encoder - 7
encoder = Dense(int(encoding_dim / 2), activation="relu")(encoder)
## Dense_layer First Decoder - 7
decoder = Dense(int(encoding_dim / 2), activation='tanh')(encoder)
## Dense_layer Second Decoder - 14
decoder = Dense(input_dim, activation='relu')(decoder)
autoencoder = Model(inputs=input_layer, outputs=decoder)
※ activity_regularizer : keras dense layer의 옵션
activity_regularizer
함수형 API 로 네트워크 층 만들기
================End================
100 epoch 사용 : 226381 * 100 의 데이터를Train 하는데 사용
batch_size 32 : 32개씩 묶어서, 1번의 계산을 함. 따라서 1 epoch마다, (226381%%32) 만큼 가중치 갱신이 일어난다.
nb_epoch = 100
batch_size = 32
autoencoder.compile(optimizer='adam',loss='mean_squared_error',metrics=['accuracy'])
autoencoder.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_5 (InputLayer) (None, 29) 0
_________________________________________________________________
dense_7 (Dense) (None, 14) 420
_________________________________________________________________
dense_8 (Dense) (None, 7) 105
_________________________________________________________________
dense_9 (Dense) (None, 7) 56
_________________________________________________________________
dense_10 (Dense) (None, 29) 232
=================================================================
Total params: 813
Trainable params: 813
Non-trainable params: 0
_________________________________________________________________
Train 상황을 지켜보기 위해, 하기 모듈을 불러와서, 사용한다.
from keras.callbacks import ModelCheckpoint, TensorBoard
## 각 iter 마다, 손실함수 값을 기록함.
checkpointer = ModelCheckpoint(filepath="D:/★2020_ML_DL_Project/Alchemy/DL_Area/model.h5",
verbose=0,
save_best_only=True)
## 서플로우가 제공하는 시각화 도구입니다.
## 이 콜백은 TensorBoard에 로그를 기록하여 학습과 테스트 측정 항목에 대한 동적 그래프나 모델 내 다양한 레이어에 대한 활성화 히스토그램을 시각화 할 수 있도록 합니다.
tensorboard = TensorBoard(log_dir='./logs',
histogram_freq=0,
write_graph=True,
write_images=True)
history = autoencoder.fit(X_train, X_train,epochs=nb_epoch,batch_size=batch_size,
shuffle=True,validation_data=(X_test, X_test),verbose=1,
callbacks=[checkpointer, tensorboard]).history
WARNING:tensorflow:From C:\ProgramData\Anaconda3\envs\test\lib\site-packages\tensorflow\python\ops\math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 226381 samples, validate on 56692 samples
Epoch 1/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.7567 - acc: 0.5776 - val_loss: 0.7468 - val_acc: 0.6296
Epoch 2/100
226381/226381 [==============================] - 16s 73us/step - loss: 0.6899 - acc: 0.6465 - val_loss: 0.7232 - val_acc: 0.6654
Epoch 3/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6767 - acc: 0.6651 - val_loss: 0.7187 - val_acc: 0.6634
Epoch 4/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6723 - acc: 0.6699 - val_loss: 0.7147 - val_acc: 0.6645
Epoch 5/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6697 - acc: 0.6746 - val_loss: 0.7114 - val_acc: 0.6737
Epoch 6/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6676 - acc: 0.6808 - val_loss: 0.7108 - val_acc: 0.6772
Epoch 7/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6663 - acc: 0.6850 - val_loss: 0.7083 - val_acc: 0.6863
Epoch 8/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6656 - acc: 0.6881 - val_loss: 0.7071 - val_acc: 0.6905
Epoch 9/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6650 - acc: 0.6899 - val_loss: 0.7066 - val_acc: 0.6873
Epoch 10/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6644 - acc: 0.6911 - val_loss: 0.7063 - val_acc: 0.6893
Epoch 11/100
226381/226381 [==============================] - 16s 73us/step - loss: 0.6641 - acc: 0.6916 - val_loss: 0.7058 - val_acc: 0.6892
Epoch 12/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6639 - acc: 0.6921 - val_loss: 0.7050 - val_acc: 0.6910
Epoch 13/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6638 - acc: 0.6930 - val_loss: 0.7060 - val_acc: 0.6895
Epoch 14/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6636 - acc: 0.6936 - val_loss: 0.7055 - val_acc: 0.6893
Epoch 15/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6633 - acc: 0.6943 - val_loss: 0.7054 - val_acc: 0.6964
Epoch 16/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6632 - acc: 0.6938 - val_loss: 0.7042 - val_acc: 0.6931
Epoch 17/100
226381/226381 [==============================] - 16s 73us/step - loss: 0.6631 - acc: 0.6949 - val_loss: 0.7049 - val_acc: 0.6905
Epoch 18/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6628 - acc: 0.6954 - val_loss: 0.7046 - val_acc: 0.6891
Epoch 19/100
226381/226381 [==============================] - 18s 79us/step - loss: 0.6628 - acc: 0.6954 - val_loss: 0.7049 - val_acc: 0.6887
Epoch 20/100
226381/226381 [==============================] - 17s 75us/step - loss: 0.6627 - acc: 0.6956 - val_loss: 0.7036 - val_acc: 0.6943
Epoch 21/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6626 - acc: 0.6959 - val_loss: 0.7053 - val_acc: 0.6867
Epoch 22/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6625 - acc: 0.6964 - val_loss: 0.7043 - val_acc: 0.6903
Epoch 23/100
226381/226381 [==============================] - 17s 73us/step - loss: 0.6623 - acc: 0.6967 - val_loss: 0.7047 - val_acc: 0.6966
Epoch 24/100
226381/226381 [==============================] - 17s 73us/step - loss: 0.6622 - acc: 0.6982 - val_loss: 0.7041 - val_acc: 0.6864
Epoch 25/100
226381/226381 [==============================] - 17s 73us/step - loss: 0.6621 - acc: 0.6973 - val_loss: 0.7041 - val_acc: 0.6935
Epoch 26/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6621 - acc: 0.6981 - val_loss: 0.7035 - val_acc: 0.6881
Epoch 27/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6620 - acc: 0.6977 - val_loss: 0.7035 - val_acc: 0.6943
Epoch 28/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6620 - acc: 0.6978 - val_loss: 0.7036 - val_acc: 0.6933
Epoch 29/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6618 - acc: 0.6979 - val_loss: 0.7069 - val_acc: 0.6904
Epoch 30/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6619 - acc: 0.6980 - val_loss: 0.7036 - val_acc: 0.6937
Epoch 31/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6618 - acc: 0.6988 - val_loss: 0.7031 - val_acc: 0.6922
Epoch 32/100
226381/226381 [==============================] - 17s 76us/step - loss: 0.6615 - acc: 0.6977 - val_loss: 0.7033 - val_acc: 0.6981
Epoch 33/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6616 - acc: 0.6986 - val_loss: 0.7035 - val_acc: 0.6921
Epoch 34/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6615 - acc: 0.6982 - val_loss: 0.7025 - val_acc: 0.6984
Epoch 35/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6614 - acc: 0.6990 - val_loss: 0.7033 - val_acc: 0.6956
Epoch 36/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6614 - acc: 0.6984 - val_loss: 0.7016 - val_acc: 0.6963
Epoch 37/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6613 - acc: 0.6992 - val_loss: 0.7017 - val_acc: 0.6994
Epoch 38/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6613 - acc: 0.6987 - val_loss: 0.7032 - val_acc: 0.6908
Epoch 39/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6612 - acc: 0.6987 - val_loss: 0.7030 - val_acc: 0.6964
Epoch 40/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6614 - acc: 0.6996 - val_loss: 0.7023 - val_acc: 0.6949
Epoch 41/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6612 - acc: 0.6991 - val_loss: 0.7026 - val_acc: 0.7002
Epoch 42/100
226381/226381 [==============================] - 16s 72us/step - loss: 0.6611 - acc: 0.6993 - val_loss: 0.7022 - val_acc: 0.7007
Epoch 43/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6612 - acc: 0.6996 - val_loss: 0.7038 - val_acc: 0.6918
Epoch 44/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6610 - acc: 0.6995 - val_loss: 0.7021 - val_acc: 0.6973
Epoch 45/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6611 - acc: 0.6997 - val_loss: 0.7019 - val_acc: 0.6941
Epoch 46/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6611 - acc: 0.6996 - val_loss: 0.7024 - val_acc: 0.6957
Epoch 47/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6611 - acc: 0.7006 - val_loss: 0.7041 - val_acc: 0.6948
Epoch 48/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6610 - acc: 0.6997 - val_loss: 0.7024 - val_acc: 0.6920
Epoch 49/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6610 - acc: 0.6996 - val_loss: 0.7023 - val_acc: 0.6942
Epoch 50/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6610 - acc: 0.6994 - val_loss: 0.7027 - val_acc: 0.6985
Epoch 51/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6609 - acc: 0.7000 - val_loss: 0.7028 - val_acc: 0.7023
Epoch 52/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6608 - acc: 0.7013 - val_loss: 0.7023 - val_acc: 0.6933
Epoch 53/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6609 - acc: 0.6999 - val_loss: 0.7011 - val_acc: 0.6973
Epoch 54/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6607 - acc: 0.7000 - val_loss: 0.7029 - val_acc: 0.6955
Epoch 55/100
226381/226381 [==============================] - 17s 73us/step - loss: 0.6607 - acc: 0.7000 - val_loss: 0.7024 - val_acc: 0.6876
Epoch 56/100
226381/226381 [==============================] - 17s 74us/step - loss: 0.6607 - acc: 0.7005 - val_loss: 0.7012 - val_acc: 0.6958
Epoch 57/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6607 - acc: 0.7008 - val_loss: 0.7021 - val_acc: 0.6952
Epoch 58/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6606 - acc: 0.7001 - val_loss: 0.7016 - val_acc: 0.6909
Epoch 59/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6607 - acc: 0.7003 - val_loss: 0.7047 - val_acc: 0.6930
Epoch 60/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6606 - acc: 0.6996 - val_loss: 0.7032 - val_acc: 0.6841
Epoch 61/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6606 - acc: 0.6998 - val_loss: 0.7040 - val_acc: 0.6896
Epoch 62/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6607 - acc: 0.6997 - val_loss: 0.7010 - val_acc: 0.6961
Epoch 63/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6605 - acc: 0.7002 - val_loss: 0.7012 - val_acc: 0.7004
Epoch 64/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6605 - acc: 0.7008 - val_loss: 0.7038 - val_acc: 0.6972
Epoch 65/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6604 - acc: 0.7010 - val_loss: 0.7008 - val_acc: 0.7032
Epoch 66/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6604 - acc: 0.7000 - val_loss: 0.7032 - val_acc: 0.7003
Epoch 67/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6604 - acc: 0.7000 - val_loss: 0.7024 - val_acc: 0.6946
Epoch 68/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6604 - acc: 0.6999 - val_loss: 0.7013 - val_acc: 0.6979
Epoch 69/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6603 - acc: 0.6997 - val_loss: 0.7014 - val_acc: 0.6973
Epoch 70/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6597 - acc: 0.6981 - val_loss: 0.6993 - val_acc: 0.7039
Epoch 71/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6588 - acc: 0.6984 - val_loss: 0.6997 - val_acc: 0.6940
Epoch 72/100
226381/226381 [==============================] - 15s 67us/step - loss: 0.6581 - acc: 0.6993 - val_loss: 0.6993 - val_acc: 0.6993
Epoch 73/100
226381/226381 [==============================] - 15s 67us/step - loss: 0.6578 - acc: 0.6985 - val_loss: 0.6991 - val_acc: 0.7017
Epoch 74/100
226381/226381 [==============================] - 15s 67us/step - loss: 0.6577 - acc: 0.6996 - val_loss: 0.6988 - val_acc: 0.6999
Epoch 75/100
226381/226381 [==============================] - 15s 67us/step - loss: 0.6574 - acc: 0.7002 - val_loss: 0.6992 - val_acc: 0.6989
Epoch 76/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6574 - acc: 0.7000 - val_loss: 0.6974 - val_acc: 0.6983
Epoch 77/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6575 - acc: 0.7002 - val_loss: 0.6992 - val_acc: 0.6979
Epoch 78/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6574 - acc: 0.7002 - val_loss: 0.6983 - val_acc: 0.6951
Epoch 79/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6574 - acc: 0.7009 - val_loss: 0.6989 - val_acc: 0.7008
Epoch 80/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6573 - acc: 0.7007 - val_loss: 0.6975 - val_acc: 0.7025
Epoch 81/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6573 - acc: 0.6995 - val_loss: 0.6979 - val_acc: 0.6936
Epoch 82/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6574 - acc: 0.6995 - val_loss: 0.6981 - val_acc: 0.6946
Epoch 83/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6573 - acc: 0.7003 - val_loss: 0.6979 - val_acc: 0.7021
Epoch 84/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6572 - acc: 0.6998 - val_loss: 0.6981 - val_acc: 0.6973
Epoch 85/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6572 - acc: 0.6992 - val_loss: 0.6992 - val_acc: 0.6941
Epoch 86/100
226381/226381 [==============================] - 17s 75us/step - loss: 0.6570 - acc: 0.6994 - val_loss: 0.6986 - val_acc: 0.6963
Epoch 87/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6573 - acc: 0.6996 - val_loss: 0.6971 - val_acc: 0.6960
Epoch 88/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6571 - acc: 0.6997 - val_loss: 0.6990 - val_acc: 0.7009
Epoch 89/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6571 - acc: 0.6995 - val_loss: 0.6976 - val_acc: 0.6993
Epoch 90/100
226381/226381 [==============================] - 15s 66us/step - loss: 0.6569 - acc: 0.7002 - val_loss: 0.6983 - val_acc: 0.6929
Epoch 91/100
226381/226381 [==============================] - 15s 66us/step - loss: 0.6570 - acc: 0.7002 - val_loss: 0.6983 - val_acc: 0.6990
Epoch 92/100
226381/226381 [==============================] - 15s 65us/step - loss: 0.6569 - acc: 0.6996 - val_loss: 0.6976 - val_acc: 0.7010
Epoch 93/100
226381/226381 [==============================] - 15s 65us/step - loss: 0.6569 - acc: 0.7002 - val_loss: 0.6978 - val_acc: 0.7008
Epoch 94/100
226381/226381 [==============================] - 15s 68us/step - loss: 0.6569 - acc: 0.7001 - val_loss: 0.7048 - val_acc: 0.6846
Epoch 95/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6569 - acc: 0.6997 - val_loss: 0.6975 - val_acc: 0.7056
Epoch 96/100
226381/226381 [==============================] - 15s 67us/step - loss: 0.6567 - acc: 0.6995 - val_loss: 0.6983 - val_acc: 0.6938
Epoch 97/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6568 - acc: 0.6989 - val_loss: 0.6983 - val_acc: 0.7041
Epoch 98/100
226381/226381 [==============================] - 16s 71us/step - loss: 0.6569 - acc: 0.6991 - val_loss: 0.7009 - val_acc: 0.6944
Epoch 99/100
226381/226381 [==============================] - 16s 70us/step - loss: 0.6567 - acc: 0.6995 - val_loss: 0.6973 - val_acc: 0.6978
Epoch 100/100
226381/226381 [==============================] - 16s 69us/step - loss: 0.6566 - acc: 0.6992 - val_loss: 0.6975 - val_acc: 0.6919
GPU 가 아닌 상황에서는 꽤나 오래걸린다….callab 으로 할껄 그랬다….로컬PC GPU 는 3G 인데…느리네…10분이상 소요
val_acc 가 0.7 이상으로 올라가지 않는모습으로 봐서, Callback 함수에서, Early Stopping 을 사용하면 더 좋을 것 같다.
EarlyStopping
from keras.callbacks import EarlyStopping
keras.callbacks.EarlyStopping(monitor=’val_acc’, min_delta=0.01, patience=5, verbose=0, mode=’max’, baseline=None, restore_best_weights=True)
autoencoder_result = load_model('D:/★2020_ML_DL_Project/Alchemy/DL_Area/model.h5')
plt.plot(history['loss'])
plt.plot(history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right');
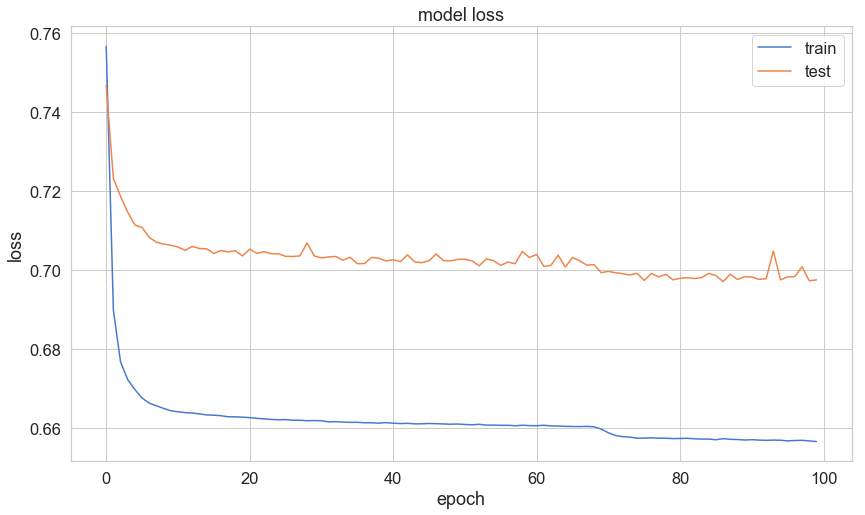
loss 값이 10 회 쯤에서, 떨어지고, 70회쯤에서도 감소한걸 볼 수 있다.
좀더 상세히 알아보기 위해 , val_data 로 사용했던, X_test 에러값을 살펴보자
print(X_test.shape)
X_test[0:3,0:5]
(56692, 29)
array([[ 1.99094864, -0.13550935, -0.25063637, 0.31893568, -0.53281644],
[ 2.08001137, -1.27448578, -1.89613731, -1.99669753, 1.30326554],
[-0.76312851, 1.52452373, 0.52515325, 0.67890148, 0.39366859]])
predictions = autoencoder.predict(X_test)
## 학습이 오래걸리지, 실제 추론 계산은 얼마 안걸림. 좀더 상세히 알아보기 위해
predictions.shape
(56692, 29)
mse = np.mean(np.power(X_test - predictions, 2), axis=1)
# mse = np.mean(np.sqrt(np.power(X_test - predictions, 2)), axis=1)
error_df = pd.DataFrame({'reconstruction_error': mse,'true_class': y_test})
error_df.describe()
| reconstruction_error | true_class | |
|---|---|---|
| count | 56692.000000 | 56692.000000 |
| mean | 0.687465 | 0.001852 |
| std | 3.137395 | 0.042997 |
| min | 0.038892 | 0.000000 |
| 25% | 0.247930 | 0.000000 |
| 50% | 0.390965 | 0.000000 |
| 75% | 0.622729 | 0.000000 |
| max | 313.437002 | 1.000000 |
from sklearn.metrics import (recall_score,confusion_matrix,classification_report,roc_curve,roc_auc_score,precision_recall_curve,auc,recall_score,
precision_recall_fscore_support)
error_df.head(3)
| reconstruction_error | true_class | |
|---|---|---|
| 269318 | 0.298731 | 0 |
| 174077 | 0.581966 | 0 |
| 3759 | 0.282954 | 0 |
error_df[error_df.true_class==1].head(3)
| reconstruction_error | true_class | |
|---|---|---|
| 82400 | 12.959438 | 1 |
| 191074 | 0.982459 | 1 |
| 42590 | 61.179662 | 1 |
auto_encoder 로 classfy 하는 핵심 아이디어 by cypision 생각
error_df 의 컨셉은 짐작해보건데, 에러값들은 기본적으로, threshold 이다. 그러니깐, 가장 적절한 threshold 값을 찾고, 이를 통해서, 측정하려는 의도로 보인다.
지금 keras로 오로지 정상거래 class=0 인것만, train 을 시켰으니, 만약 학습이 완벽하다면,
class 1에 대해서는 에러값이 class=0 일때보다 훨씬, 두드러지게 클 것이다.
그래서, mse = np.mean(np.power(X_test - predictions, 2), axis=1) 에 대해서 , sqrt 도 안한것 같다. 나름 좋은 아이디어로 보인다. 참신하다. 진짜.
## y_score 자리에는 labe 값 뿐아니라, estimate probability 값도 올 수 있다.
fpr, tpr, thresholds = metrics.roc_curve(y_true=error_df.true_class, y_score=error_df.reconstruction_error)
roc_auc = auc(fpr, tpr)
len(thresholds)
print(fpr[0:3],tpr[0:3],thresholds[0:3])
[0.00000000e+00 1.76719034e-05 1.76719034e-05] [0. 0. 0.00952381] [314.4370016 313.4370016 284.31621498]
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, label='AUC = %0.4f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.001, 1])
plt.ylim([0, 1.001])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show();
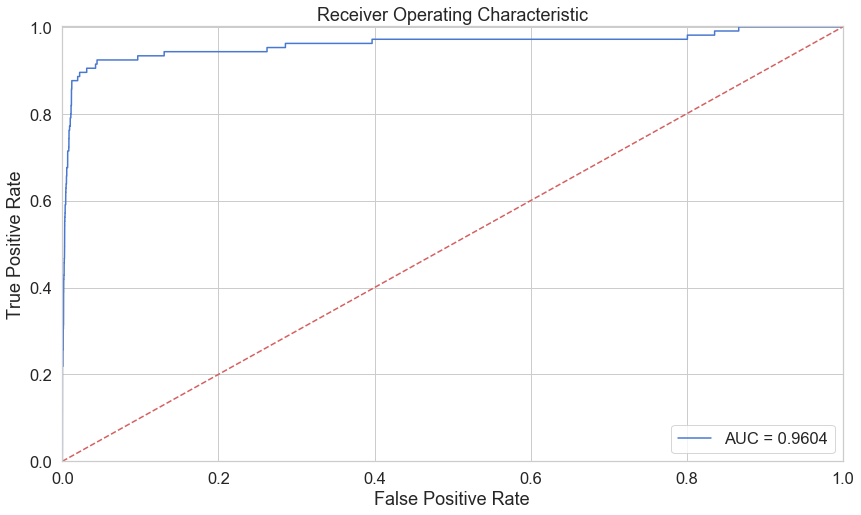
While our results look pretty good, we have to keep in mind of the nature of our dataset. ROC doesn’t look very useful for us. Onward…
근데 이 커브 곡선으로 진짜, 모델성능이 좋은지도…그리고, threshold값을 뭘로 해야 하는지도 잘 모르겠다.
precision, recall, th = precision_recall_curve(error_df.true_class, error_df.reconstruction_error)
plt.plot(recall, precision, 'b', label='Precision-Recall curve')
plt.title('Recall vs Precision')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.show()
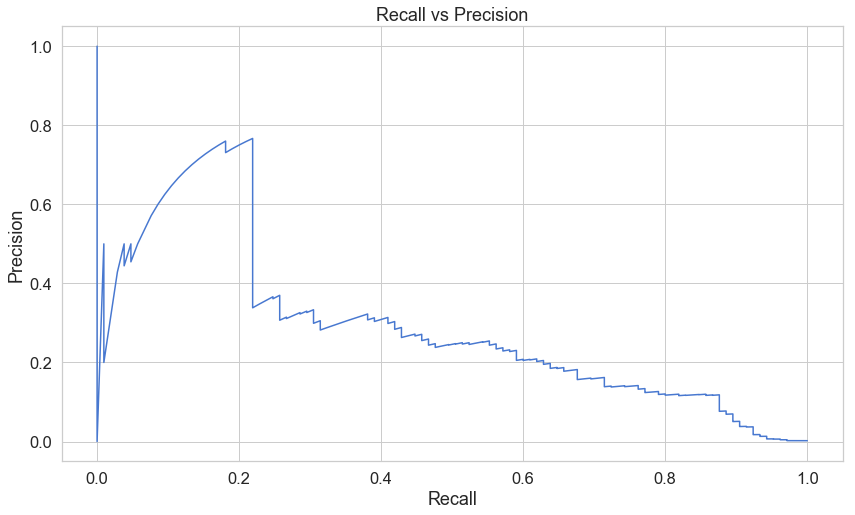
print(precision.shape)
print(len(precision),len(recall),len(th)) ## th 결과값이 하나 더 적다
(48592,)
48592 48592 48591
plt.plot(th, precision[1:], 'b', label='Threshold-Precision curve')
plt.title('Precision for different threshold values')
plt.xlabel('Threshold')
plt.ylabel('Precision')
plt.show()
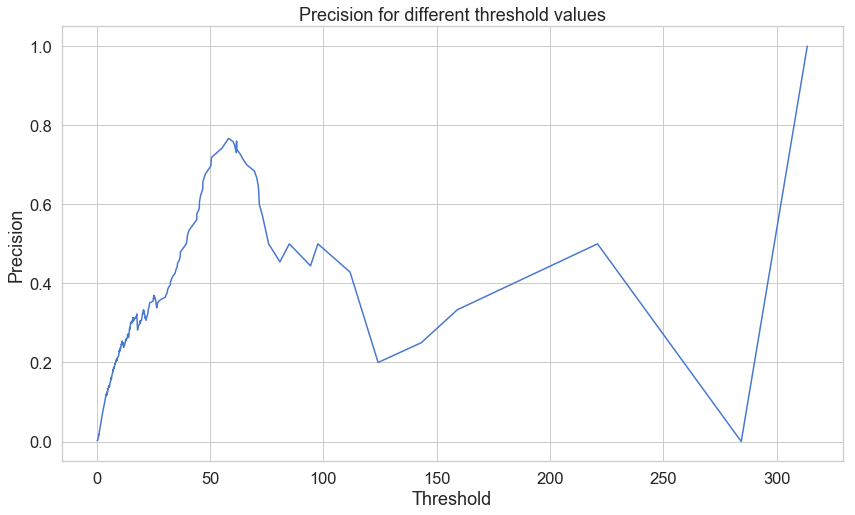
plt.plot(th, recall[1:], 'b', label='Threshold-Recall curve')
plt.title('Recall for different threshold values')
plt.xlabel('Threshold')
plt.ylabel('Recall')
plt.show()
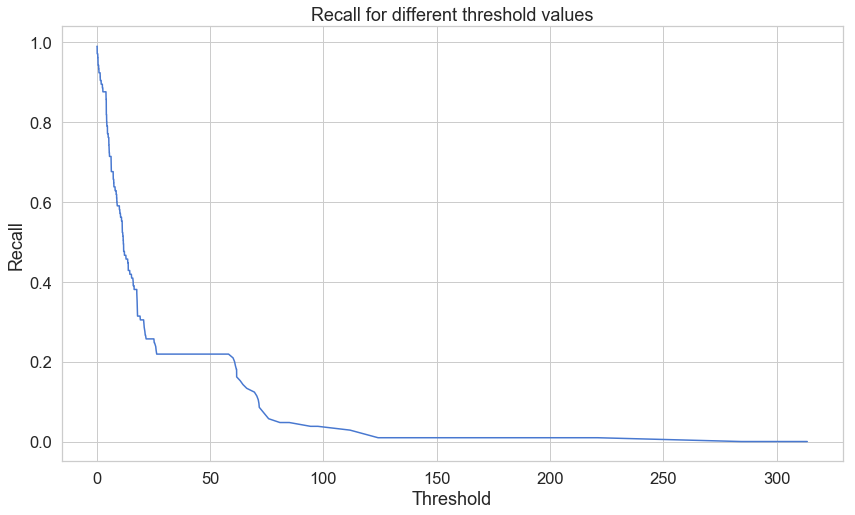
내가 볼때는 대략 threshold 값이 60 일때,
Precision : 0.74 대략…
Recall : 0.21 대랙 으로..제일 좋은 시점이 아닌가 싶다. 원저자는 threshold = 2.9 로 했다.
threshold_00 = 2.9
threshold_01 = 60.0
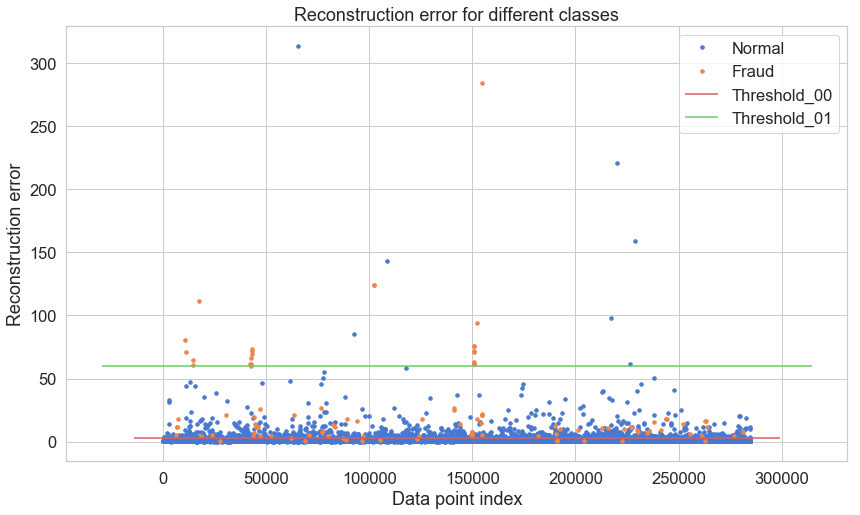
groups = error_df.groupby('true_class')
fig, ax = plt.subplots()
for name, group in groups:
ax.plot(group.index, group.reconstruction_error, marker='o', ms=3.5, linestyle='',
label= "Fraud" if name == 1 else "Normal")
ax.hlines(threshold_00, ax.get_xlim()[0], ax.get_xlim()[1], colors="r", zorder=100, label='Threshold_00')
ax.hlines(threshold_01, ax.get_xlim()[0], ax.get_xlim()[1], colors="g", zorder=100, label='Threshold_01')
ax.legend()
plt.title("Reconstruction error for different classes")
plt.ylabel("Reconstruction error")
plt.xlabel("Data point index")
plt.show();
y_pred = [1 if e > threshold_00 else 0 for e in error_df.reconstruction_error.values]
conf_matrix = confusion_matrix(error_df.true_class, y_pred)
target_names = ['normal','fraud']
print(classification_report(error_df.true_class,y_pred,target_names=target_names))
precision recall f1-score support
normal 1.00 0.98 0.99 56587
fraud 0.08 0.88 0.15 105
micro avg 0.98 0.98 0.98 56692
macro avg 0.54 0.93 0.57 56692
weighted avg 1.00 0.98 0.99 56692
y_pred = [1 if e > threshold_01 else 0 for e in error_df.reconstruction_error.values]
conf_matrix = confusion_matrix(error_df.true_class, y_pred)
target_names = ['normal','fraud']
print(classification_report(error_df.true_class,y_pred,target_names=target_names))
precision recall f1-score support
normal 1.00 1.00 1.00 56587
fraud 0.77 0.22 0.34 105
micro avg 1.00 1.00 1.00 56692
macro avg 0.88 0.61 0.67 56692
weighted avg 1.00 1.00 1.00 56692
threshold 값을 표현되었지만, 사실 이 값은 reconstruction_error 이다. sqrt 하지 않은 mse 이다. 이 기준값을 threshold 로 하는건데…
(threshold_00 : 원 저자의 threshold vs threshold_01 : cypision(본인) 의 threshold)
솔직히 왜 원저자는 2.9 로 했는지 모르겠다. 실제 그래프도 내가 실습한거와 비슷한 모양인데. 뭔가 이유가 있을것 같은데..나는 모르겠다.
일단, 내가 잡은 에러값기준, 60 이 좀더, fraud 기준으로 f1-score 가 더 좋다. 여기까지만이다.
하기는 Keras 의 Sequantial 클래스를 이용하여 모델을 구성한것임 - 참고용
Sequatial Class 로 네트워크 층 만들기
================Start================
from keras import models
from keras import layers
input_dim = X_train.shape[1]
## input_layer
model_S = models.Sequential()
## Dense_layer first Encoder - 14
model_S.add(layers.Dense(14,activation="tanh",activity_regularizer=regularizers.l1(10e-5)))
## Dense_layer Second Encoder - 7
model_S.add(layers.Dense(7,activation="relu"))
## Dense_layer First Decoder - 7
model_S.add(layers.Dense(7,activation='tanh'))
## Dense_layer Second Decoder - 14
model_S.add(layers.Dense(14,activation='relu'))
Sequatial Class 로 네트워크 층 만들기
================End================
summary
normal 데이터만을 학습하고, 이를 최적화 시킨다. 이제 encoder1-encoder2-decoder1-decoder1 구성으로 loss 함수를 MSE 로 한다. (autoencoder.compile(optimizer=’adam’,loss=’mean_squared_error’,metrics=[‘accuracy’]))
test 데이터나, 실제 데이터가 들어오게 되면, 에러값이 정상데이터보다 훨씬 커지게 출력된다. precision, recall 값 들을 시각화하여, 최대로 하는 적절한 에러값을 찾고, 이를 threshold 값으로 정한다. 정해진 threshold 값을 기준으로 classfication 한다.
※ [통상 auto encoder의 계층모습 : encoder - Latent vector - decoder]

Comments