Text Analyis using RNN and LSTM in keras

import keras
keras.__version__

Using TensorFlow backend.

'2.2.4'

RNN recurrent neural networks

케라스의 순환 층

넘파이로 간단하게 구현한 과정이 실제 케라스의 SimpleRNN 층에 해당한다. 먼저 numpy 로 개념을 잡고, 실습으로 들어가자

Numpy 로 개념잡기

import numpy as np

timesteps = 100 # 1개 sample 의 sequence 로 이해하면 된다.
input_features = 32 # 입력특성의 차원인데...실전에서는 embedding dim 정도
output_features = 64 # 출력차원의 특성 별 의미없다. 그냥 정한거다 예제에선.. 32로 바꿔도 된다...

inputs = np.random.random((timesteps,input_features))
state_t = np.zeros((output_features,))
print(inputs.shape,'\t',state_t.shape,state_t.ndim)

(100, 32) 	 (64,) 1

포인트는 가중치 행렬이 기존의 W 외에, U 가 1개 더 있다는 점이다.

W = np.random.random((output_features,input_features))
U = np.random.random((output_features,output_features))
b = np.random.random((output_features,))

print("W.shape:{}\tU.shape:{}\tb.shape:{}".format(W.shape,U.shape,b.shape))

W.shape:(64, 32)	U.shape:(64, 64)	b.shape:(64,)

successive_outputs = []
for input_t in inputs:
    output_t = np.tanh(np.dot(W,input_t)+np.dot(U,state_t)+b)
    successive_outputs.append(output_t)
    state_t = output_t # t+1 때 사용할 상태(hidden) 값을 현재 구한 값으로 교체함
    
final_output_sequence = np.stack(successive_outputs,axis=0)

final_output_sequence.shape

(100, 64)

상기 Numpy 에서, 중요한 포인트는 가중치 행렬 U 의 등장과, output 를 출력할때, 활성화 함수 안에, 과거(t-1) 출력값을 이용한다는 점이다.
수식으로 보면, t-1 만의 직전값이 들어가지만, t-1 은 결국 t-2 의 값이 반영되어 있기 때문에 과거의 값을 반영한다고 보면된다.

keras SimpleRNN

from keras.layers import SimpleRNN

SimpleRNN이 한 가지 다른 점은 넘파이 예제처럼 하나의 시퀀스가 아니라 다른 케라스 층과 마찬가지로 시퀀스 배치를 처리한다는 것.
즉, (timesteps, input_features) 크기가 아니라 (batch_size, timesteps, input_features) 크기의 입력을 받는다

케라스에 있는 모든 순환 층과 동일하게 SimpleRNN은 두 가지 모드로 실행할 수 있다.

1. 각 타임스텝의 출력을 모은 전체 시퀀스를 반환(크기가 (batch_size, timesteps, output_features)인 3D 텐서) return_sequences=False (True)
2. 입력 시퀀스에 대한 마지막 출력만 반환(크기가 (batch_size, output_features)인 2D 텐서). return_sequences=False (default)

from keras.models import Sequential
from keras.layers import Embedding, SimpleRNN

## 마지막 출력만 반환하는 case return_sequences=False
model = Sequential()
model.add(Embedding(10000, 32)) ## (batch_size, (sample의 sequence 길이)max_len, 32) 의 3D tensor 가 출력된다.
model.add(SimpleRNN(32))
model.summary()

WARNING:tensorflow:From C:\ProgramData\Anaconda3\envs\test\lib\site-packages\tensorflow\python\framework\op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_1 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, 32)                2080      
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0
_________________________________________________________________

## 전체 출력만 반환하는 case return_sequences=True
model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_2 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_2 (SimpleRNN)     (None, None, 32)          2080      
=================================================================
Total params: 322,080
Trainable params: 322,080
Non-trainable params: 0
_________________________________________________________________

네트워크의 표현력을 증가시키기 위해 여러 개의 순환 층을 차례대로 쌓는 것이 유용할 때가 있습니다. 이런 설정에서는 중간 층들이 전체 출력 시퀀스를 반환하도록 설정해야 합니다:

model = Sequential()
model.add(Embedding(10000, 32))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32))  # 맨 위 층만 마지막 출력을 반환합니다.
model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_3 (Embedding)      (None, None, 32)          320000    
_________________________________________________________________
simple_rnn_3 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_4 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_5 (SimpleRNN)     (None, None, 32)          2080      
_________________________________________________________________
simple_rnn_6 (SimpleRNN)     (None, 32)                2080      
=================================================================
Total params: 328,320
Trainable params: 328,320
Non-trainable params: 0
_________________________________________________________________

IMDB 로 활용해보기

from keras.datasets import imdb
from keras import preprocessing

# 특성으로 사용할 단어의 수
max_features = 10000
# 사용할 텍스트의 길이(가장 빈번한 max_features 개의 단어만 사용합니다)
maxlen = 500
batch_size = 32

## numpy version 문제로, imdb.load 가 수행되지 않는 경우가 있다. 
# save np.load
np_load_old = np.load
# modify the default parameters of np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)

# call load_data with allow_pickle implicitly set to true
# 정수 리스트로 데이터를 로드합니다.
print('데이터 로딩...')
(input_train, y_train), (input_test, y_test) = imdb.load_data(num_words=max_features)
# restore np.load for future normal usage (다시 numpy.load 를 원래데로 원복한다.)
np.load = np_load_old

데이터 로딩...

print(len(input_train), '훈련 시퀀스')
print(len(input_test), '테스트 시퀀스')

25000 훈련 시퀀스
25000 테스트 시퀀스

print('시퀀스 패딩 (samples x time=sequnece length)')
input_train = sequence.pad_sequences(input_train, maxlen=maxlen) # 지난번에 04_keras_01 에서 봤다시피...뒤에서 [-500:] 으로 끊어온다.
input_test = sequence.pad_sequences(input_test, maxlen=maxlen)
print('input_train 크기:', input_train.shape)
print('input_test 크기:', input_test.shape)

시퀀스 패딩 (samples x time=sequnece length)
input_train 크기: (25000, 500)
input_test 크기: (25000, 500)

Embedding 층과 SimpleRNN 층을 사용해 간단한 순환 네트워크를 훈련시켜 보겠습니다:

from keras.layers import Dense

model = Sequential()
model.add(Embedding(max_features, 32))
model.add(SimpleRNN(64)) ## 32로 하든 64로 하든 큰 차이 없다. 예제에서는 32 였지만...필자가 어떤의미로 32 했는지 궁금해서 바꾸어서 돌렸다.
model.add(Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['acc'])
history = model.fit(input_train, y_train,
                    epochs=10,
                    batch_size=128,
                    validation_split=0.2)

WARNING:tensorflow:From C:\ProgramData\Anaconda3\envs\test\lib\site-packages\tensorflow\python\ops\math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 20000 samples, validate on 5000 samples
Epoch 1/10
20000/20000 [==============================] - 18s 918us/step - loss: 0.6097 - acc: 0.6592 - val_loss: 0.5038 - val_acc: 0.7640
Epoch 2/10
20000/20000 [==============================] - 16s 796us/step - loss: 0.3965 - acc: 0.8305 - val_loss: 0.4357 - val_acc: 0.8050
Epoch 3/10
20000/20000 [==============================] - 16s 794us/step - loss: 0.3275 - acc: 0.8676 - val_loss: 0.4275 - val_acc: 0.8308
Epoch 4/10
20000/20000 [==============================] - 16s 803us/step - loss: 0.3377 - acc: 0.8735 - val_loss: 0.4020 - val_acc: 0.8342
Epoch 5/10
20000/20000 [==============================] - 16s 796us/step - loss: 0.2580 - acc: 0.8996 - val_loss: 0.3622 - val_acc: 0.8732
Epoch 6/10
20000/20000 [==============================] - 16s 807us/step - loss: 0.4353 - acc: 0.8347 - val_loss: 0.5364 - val_acc: 0.7428
Epoch 7/10
20000/20000 [==============================] - 16s 808us/step - loss: 0.2791 - acc: 0.8958 - val_loss: 0.4061 - val_acc: 0.8246
Epoch 8/10
20000/20000 [==============================] - 16s 804us/step - loss: 0.2001 - acc: 0.9248 - val_loss: 0.4141 - val_acc: 0.8448
Epoch 9/10
20000/20000 [==============================] - 16s 810us/step - loss: 0.1667 - acc: 0.9360 - val_loss: 0.4292 - val_acc: 0.8372
Epoch 10/10
20000/20000 [==============================] - 16s 800us/step - loss: 0.1567 - acc: 0.9421 - val_loss: 0.4943 - val_acc: 0.7910

import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(1, len(acc) + 1)

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

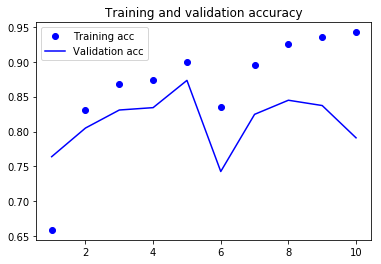
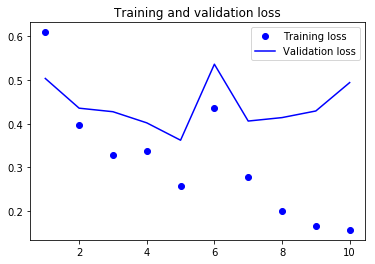
RNN(32) 로 했을때보다는 수렴이 좀 안되긴 한다….특시 6 epoch 가 좀 이상하기도 하고….일단, 실전에서는 RNN 을 사용하지 않으니깐
결과가, 눈에 띄게 좋아지지는 않는다는걸 기억하고, 넘어간다.

LSTM (Long Short Term Memory)

• Simple RNN 의 단점인, Grdient vanishing , Grdient Explode 를 피하기 위해 만들어졌다.
• 크게는 RNN 의 변형으로 봐도 무방하다

LSTM 은 확실히 책만으로 어려워서, 하기의 주소를 참고했다.
minsuk-heo youtube
terry uhm youtube
위 두분이 모두 참고했고, 내가볼때, LSTM 설명의 Bible 같은 Blog (http://colah.github.io/posts/2015-08-Understanding-LSTMs/)

기본 컨셈은 RNN 의 h 외에, Cell 이란 개념이 등장하고, 이를 구하는 것이 핵심이다.
Cell 은 메모리라 할 수 있는데, 과거 정보를 기억할것은 일부만 기억하고(나머지는 forget한다) 현재 구해지는 값을 조절하여 h 와 더불어 Cell 로 유지한다.
이로 인해서 심플 RNN 보다, parameter 행렬이 4배로 늘었으며, 계산량이 많아졌다. 게다가, ‘gate’ 란 개념이 생겼음을 명심해야 한다.

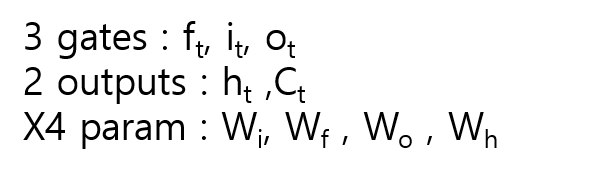
f : forget 하는 비율을 조정하는 gate
i : input 하는 비율을 조정하는 gate
o : output 하는 비율을 조정하는 gate
W -i,f,o,h 는 상기 게이ㅡ와 hidden 의 파라미터 행렬임을 명심해야 한다.

LSTM 의 모습

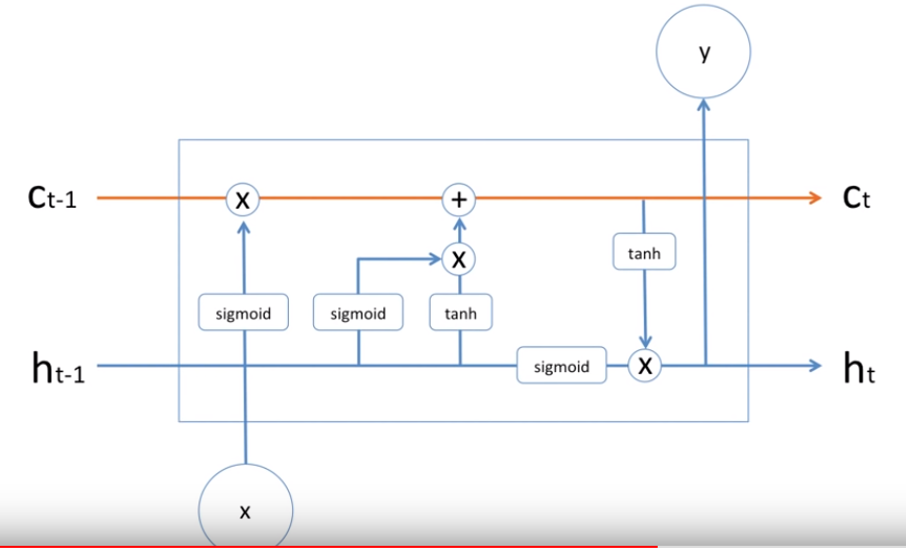
하기 구조를 한개씩 살펴보자. Ct 개념이 LSTM 의 핵심이니, 흐름을 Ct 중심으로 따라간다.
먼저 과거의 Cell(t-1) 의 값 앞에 ft 가 있는데, 이는 forget gate 값이고, forget gate 값 역시 ACTIVATION(WX+B) 으로 구해진다.
여기서 ACTIVATION 함수가 sigmoid (0~1) 이니, 나오는 값은 확률로 해석하여, 과거의 값을 몇 % 만 남기는 지에 대한 설명이라 할 수 있다.

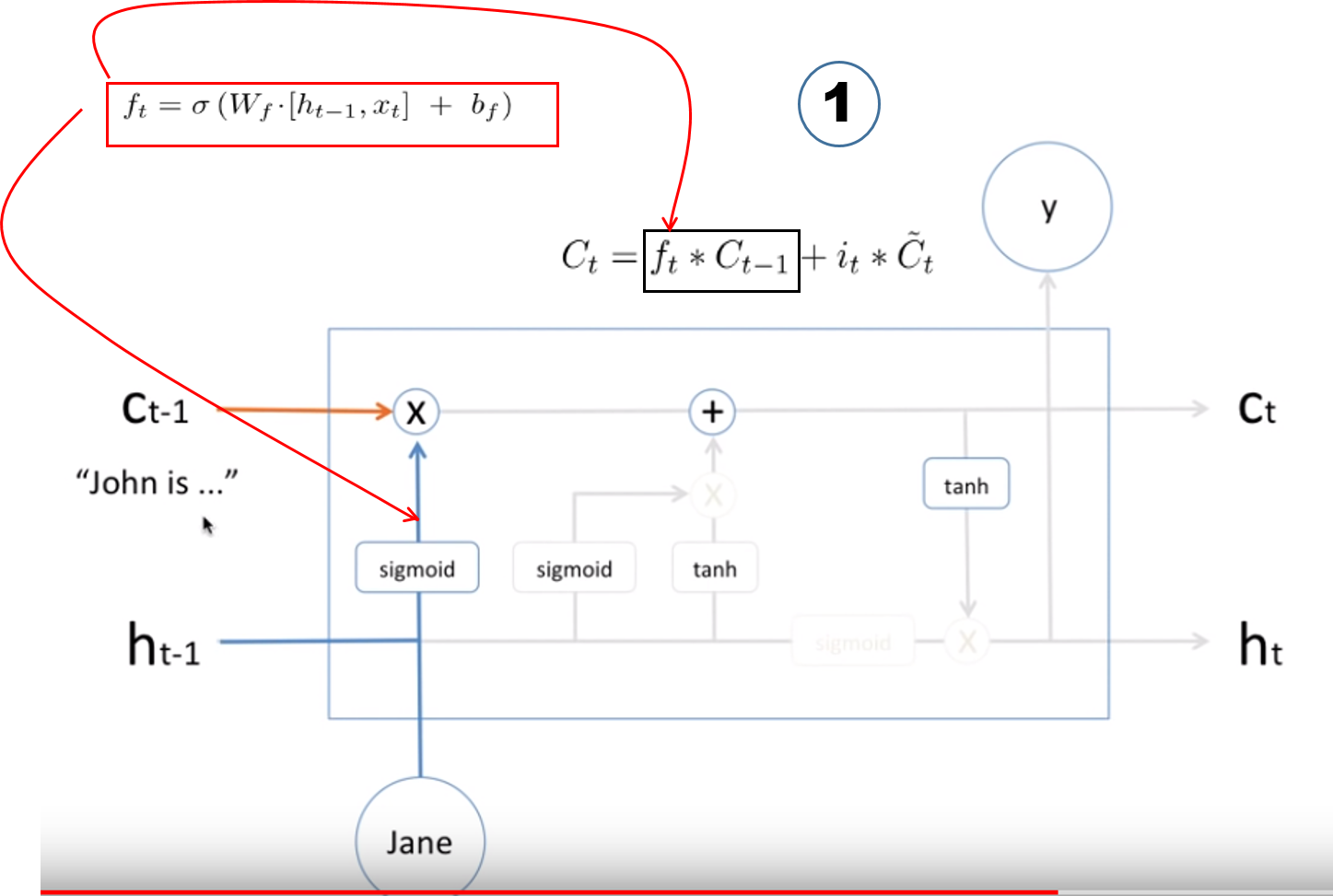
Ct 개념이 LSTM 의 핵심이니, 흐름을 Ct 중심으로 따라간다. Cell(hat t)
Ct 를 구성하는 뒷부분을 보면 Cell(hat t) 의 값 앞에 it 가 있는데, 이는 input gate 값이고, input gate 값 역시 ACTIVATION(WX+B) 으로 구해진다.
여기서 ACTIVATION 함수가 sigmoid (0~1) 이니, 나오는 값은 확률로 해석하여, 현재 들어온 x 데이터의 Cell(hat t) 값의 몇 % 만 input 넣는지에 대한 비율이다.
Cell(hat t) 는 input gate 만들때 사용하는 변수들과 동일한 변수들을 사용하는데 , ACTIVATION 함수만 tanh 로 다르다.
여기까지가, Cell 값을 구하는 과정이다.

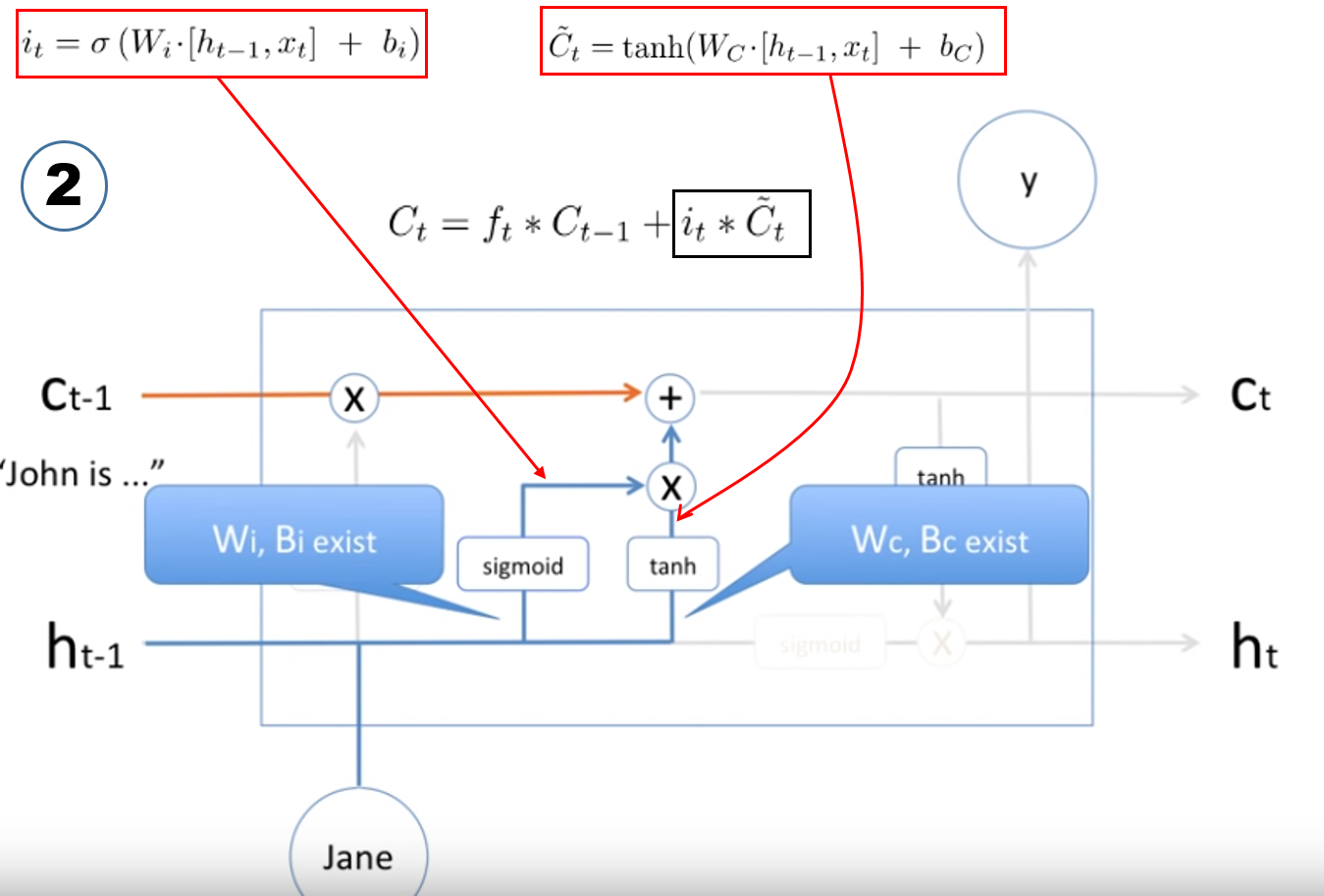
하기 그림은 파란색을 주목해서 보면된다.
위 설명에서, Cell 값은 구성을 보여줬고, 남은 것은 hidden state 상태 값과, 실제 출력 값이다.
이 둘은 같은 값을 가진다, 마지막 남은 output gate 가 사용되어진다.

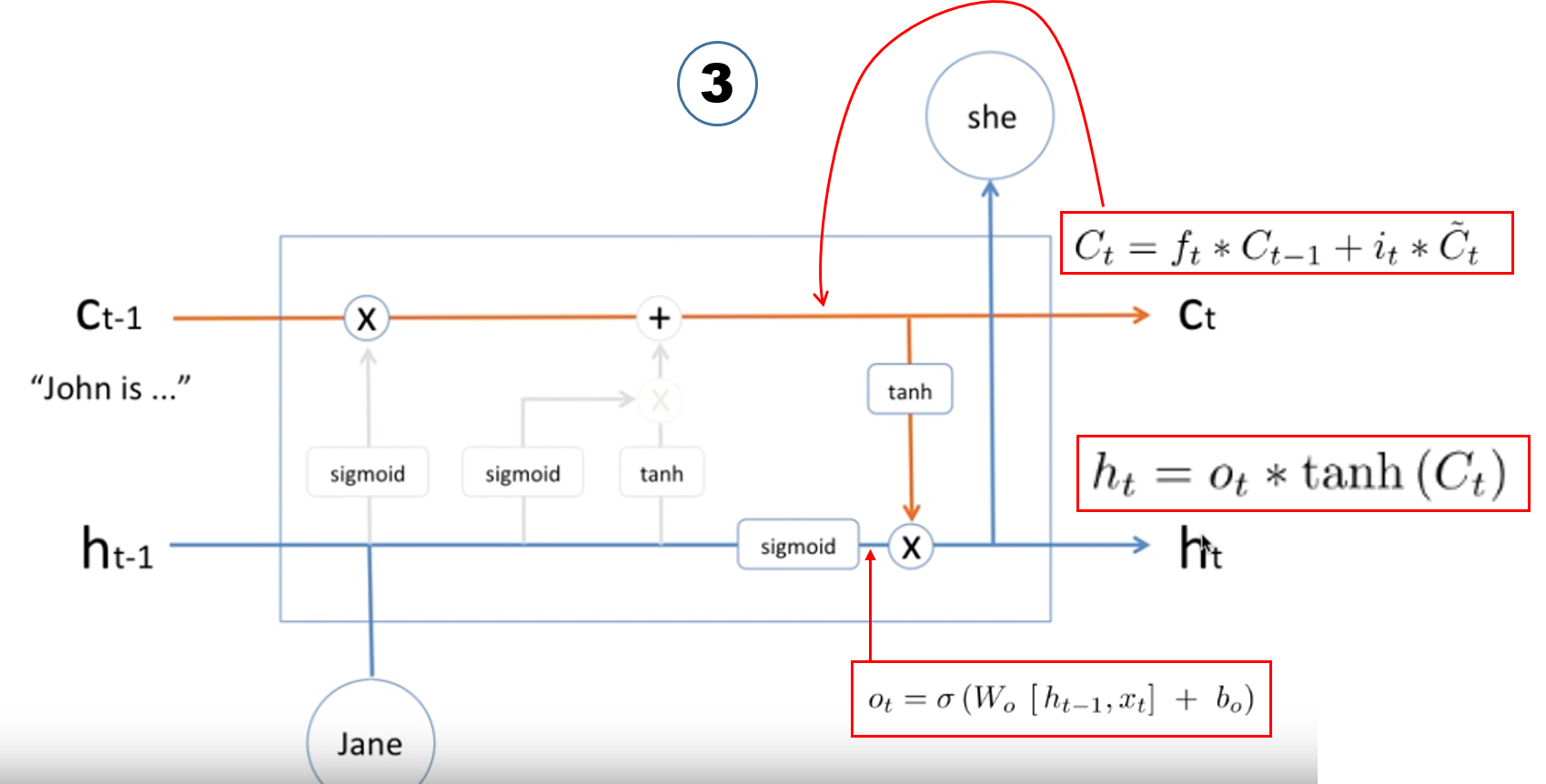
keras LSTM

from keras.layers import LSTM

model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32)) # LSTM 도, return_sequences  를 가진다. 32는 units: Positive integer, dimensionality of the output space. 이다.
model.add(Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['acc'])
history = model.fit(input_train, y_train,
                    epochs=10,
                    batch_size=128,
                    validation_split=0.2)

Train on 20000 samples, validate on 5000 samples
Epoch 1/10
20000/20000 [==============================] - 69s 3ms/step - loss: 0.5019 - acc: 0.7611 - val_loss: 0.4203 - val_acc: 0.8338
Epoch 2/10
20000/20000 [==============================] - 70s 3ms/step - loss: 0.2995 - acc: 0.8845 - val_loss: 0.3349 - val_acc: 0.8514
Epoch 3/10
20000/20000 [==============================] - 69s 3ms/step - loss: 0.2310 - acc: 0.9140 - val_loss: 0.2792 - val_acc: 0.8890
Epoch 4/10
20000/20000 [==============================] - 70s 4ms/step - loss: 0.2032 - acc: 0.9245 - val_loss: 0.4937 - val_acc: 0.8212
Epoch 5/10
20000/20000 [==============================] - 70s 3ms/step - loss: 0.1799 - acc: 0.9358 - val_loss: 0.2854 - val_acc: 0.8846
Epoch 6/10
20000/20000 [==============================] - 69s 3ms/step - loss: 0.1542 - acc: 0.9453 - val_loss: 0.2999 - val_acc: 0.8820
Epoch 7/10
20000/20000 [==============================] - 72s 4ms/step - loss: 0.1433 - acc: 0.9471 - val_loss: 0.3388 - val_acc: 0.8600
Epoch 8/10
20000/20000 [==============================] - 69s 3ms/step - loss: 0.1270 - acc: 0.9559 - val_loss: 0.4320 - val_acc: 0.8768
Epoch 9/10
20000/20000 [==============================] - 72s 4ms/step - loss: 0.1163 - acc: 0.9599 - val_loss: 0.4053 - val_acc: 0.8568
Epoch 10/10
20000/20000 [==============================] - 70s 3ms/step - loss: 0.1119 - acc: 0.9600 - val_loss: 0.3822 - val_acc: 0.8654

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(1, len(acc) + 1)

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

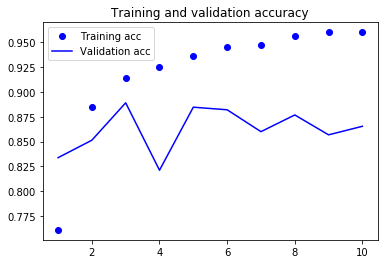
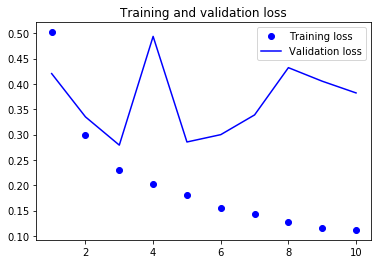
결과가 더 좋아지기 위해서는 parmeter tunning 과, 규제를 추가하는 등의 작업이 남아있다.
그러나, 리뷰를 전체적으로 길게 분석하는 것이 감성분류문제에 적합하지 않기 때문에… 결과가 엄청 난것은 아니라고, 책에서 언급되어있다.