Gradient Boosting TREE Classification
Reference
- StatQuest with Josh Starmer youtube
- StatQuest 기존강의를 정리한 다른 이의 Blog Posting (https://dailyheumsi.tistory.com)
RandomForest, Adaboost, GBTR(Regression) 정리함
이번 글에서는, Boosting 중, 비교적 최근에 많이 쓰이는 Gradient Boost 에 대해 정리해보려고 한다.
Kaggle 에서 많이보이는 XGboost 와 Light GBM 이 Gradient Boost 를 바탕으로 나온 모델이다.
사실상 현재 제일 많이쓰이는 Tree 계열의 모델을 이해하는데 기초적인 지식을 쌓는다고 볼 수 있다.
단, 기존의 Adaboost 와 GBTR 은 참조의 Blog에 정리가 잘 되어있으니, 그 글을 읽으면 되고, 여기서는 거기서 다루지 않은 것들에 대해서, 추가로 정리한다.
기존적인 내용은 youtube StatQuest 강의 화면 캡쳐이다.
Gradient Boost Regression 요약
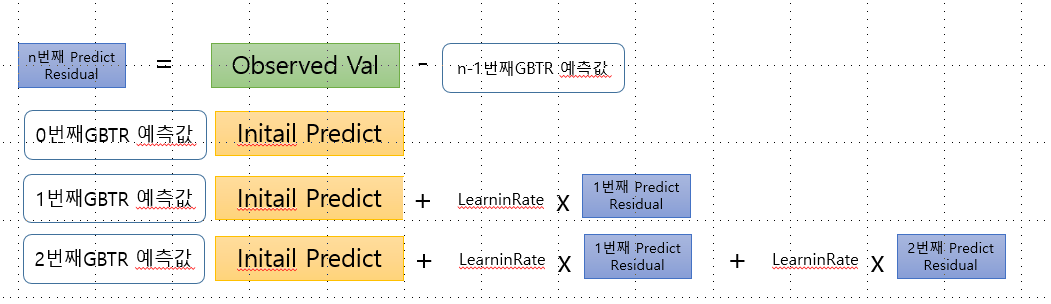
- One Leaf None : 모든 데이터의 평균값으로 initail predict 값이 설정됨
- 오차에 대한 학습 Concept
1) (Observed Value - initail predict) = 1번째 residual
2) 1번째 Tree 생성(Tree01) : 주로 leaf 8 ~32 짜리의 트리 사용. 분기할 Node 기준은 Leaste Square Error 를 지향하는 기준으로 선택됨. (regression이기 때문. Classify면 Gini Impurity같은거)
3) 1번째 Tree 로 실제 data 예측하기 : 실제 Data 값으로 예측하면1번째 residual중 1개의 값이 나올 것임(같은 leaf내에서는 평균값). 왜냐하면1번째 residual를 예측하는 하는 모델이기 때문이다. 약간 임시적인 value (residual) 인데, 이것이 4) 과정을 거치면서 진찌 실전용 예측값이 나오게 된다.
4) 3)에 learning rate(i.e 0.3) 를 곱해서 initail predict 에 더하면, 이 값이 곧 1번째 Tree로부터 도출된 예측값이다.
Node Selection(Feature Selection)
Gini 같은 Gain 이론을 사용하냐 또는 leaf 평균값의 SumOfSquaredResidual: SSR 을 비교하느냐는 오로지 구하고자 하는 값이 Classification 인가 Regression 인가에 달려있다. 헷갈리지 말자
Regression 모델이면, Feature node 가 category01 라도, 자식Noede 들의 SRR 을 구하고, 다른 category02 컬럼이나,
Numeric 컬럼의 SSR 값과 비교하여 SSR 이 적은것으로 선택하면 되는 것이다.
물론, Numeric 컬럼 이라면, 가장 Best 구간을 찾기위한 탐색이 먼저 이루어진다는 전제하에서다.
Regression Trees, Clearly Explained!!!
Gradient Boost Classify
컨셉은 Regression 과 비슷하다. 단, 이거는 Classify 이기 때문에 예측값은 Probability 이다.
1.초기값 설정
불가피하게 Log(odds) 개념을 얘기할 수 밖에 없는데, 이 부분은 다른 Posting 을 통해 다루도록 하겠다.
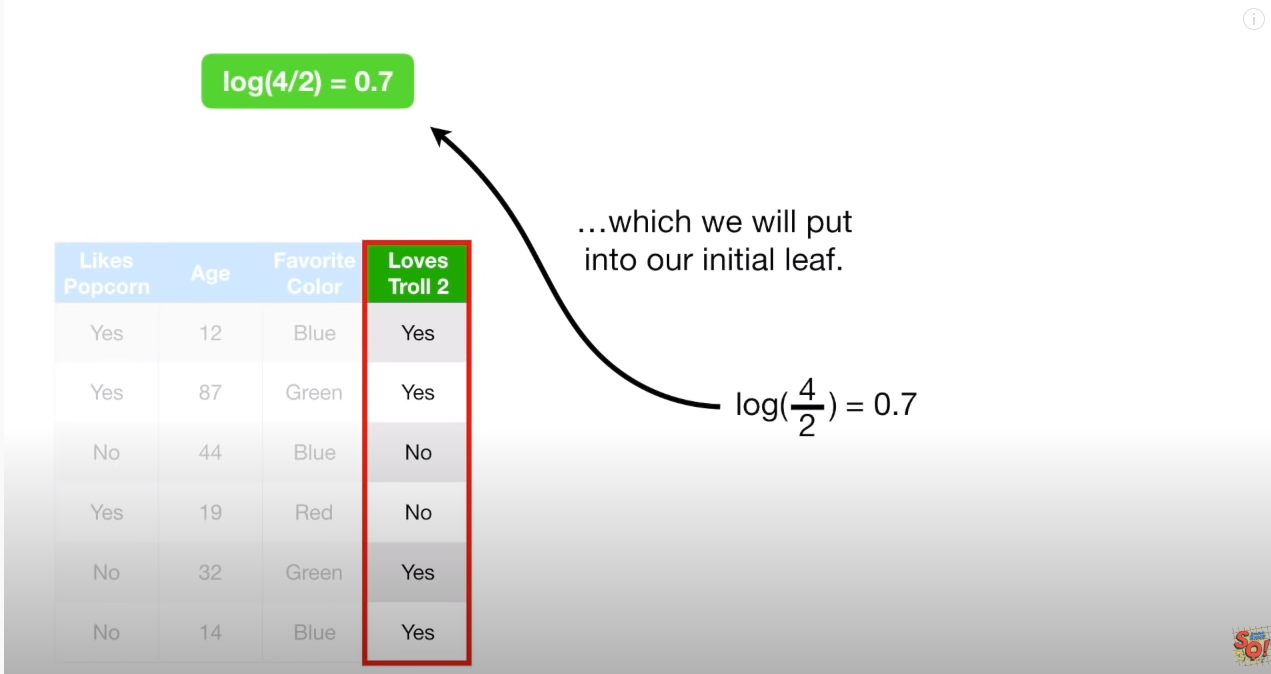
우선 분류값 Yes = 1 에 대한 Log(odds) 값을 구한다. (Log(odds)는 카테고리 변수의 독립성검증에서도 사용되며, logistic regression 과도 연관이 있다)
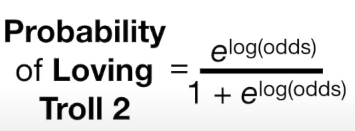
Log(odds) 를 사용하는 이유는 추측컨데, Log(odds) 자체가 logistic function과도 다아있기 때문으로 보인다. Log(odds)는 logistic Funtion 의 P(확률) 값으로 변환하기 쉽기 때문이다.
0.7 을 얻게된다. 즉 초기 확률값은 0.7 이고, 주로 threshold 값이 0.5 인걸 볼때, 모든 분류를 yes로 분류하는 분류기(initial predict) 임을 알 수 있다.
2. 초기 예측값으로 오차를 구하고 오차를 학습하는 Tree 생성하기
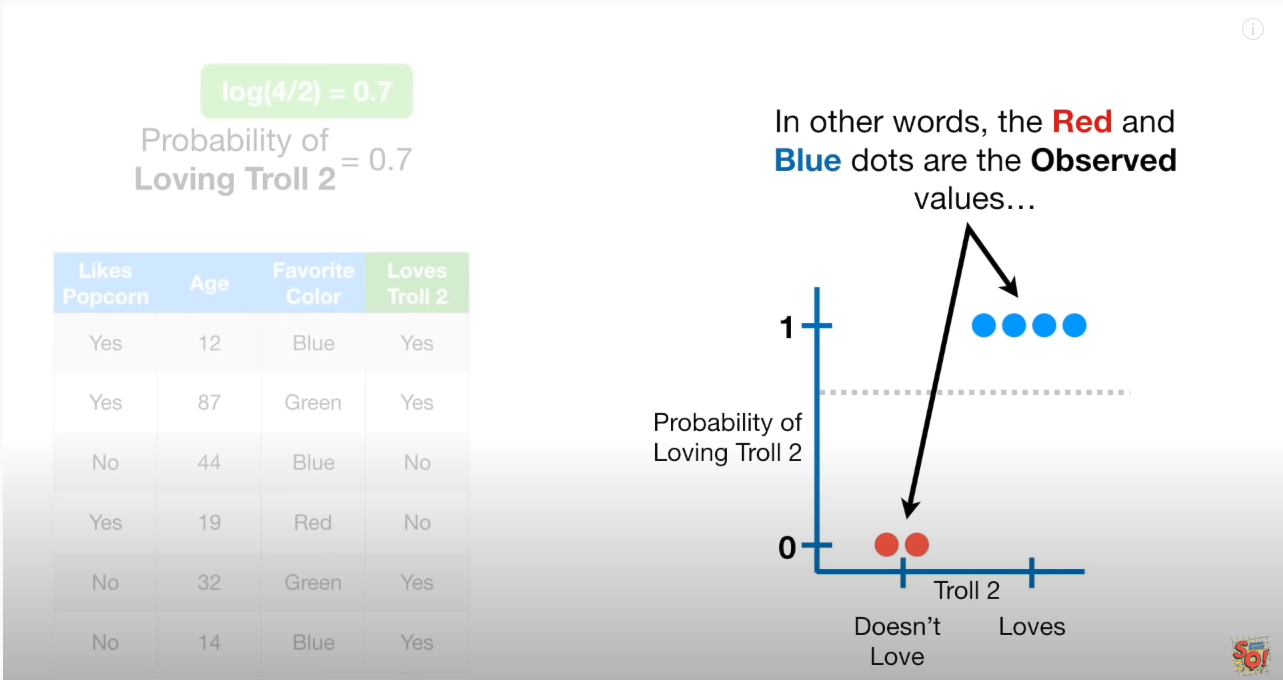
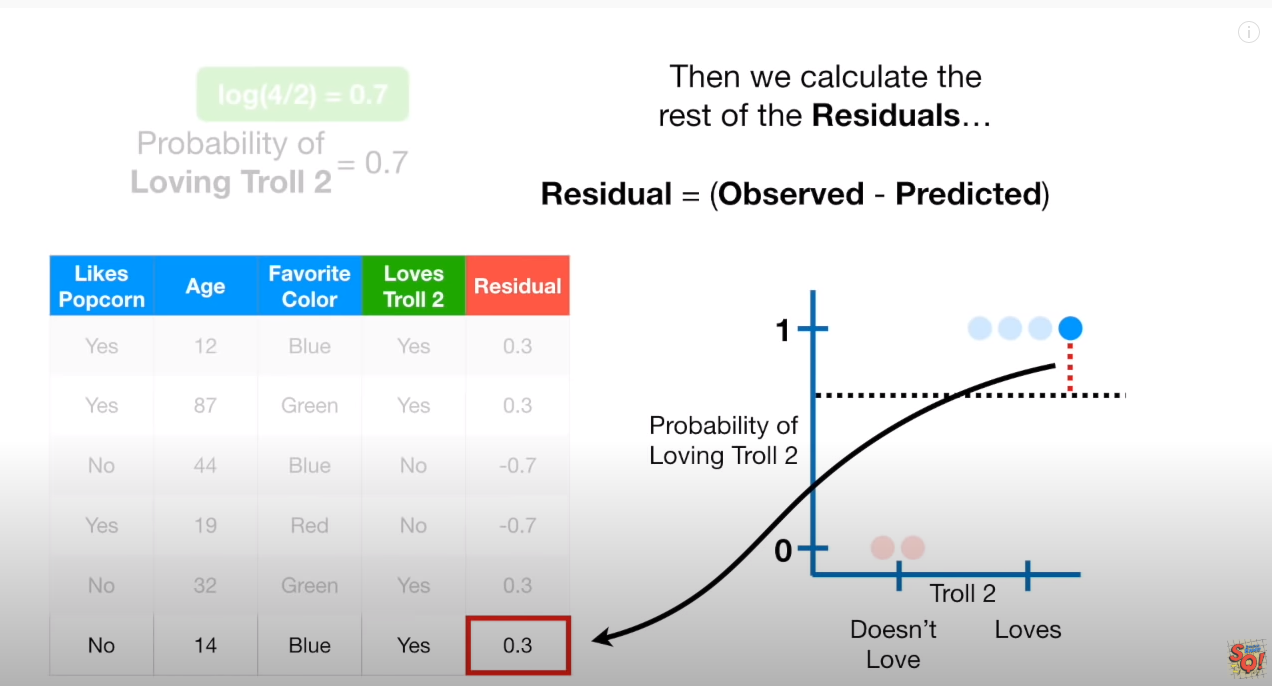
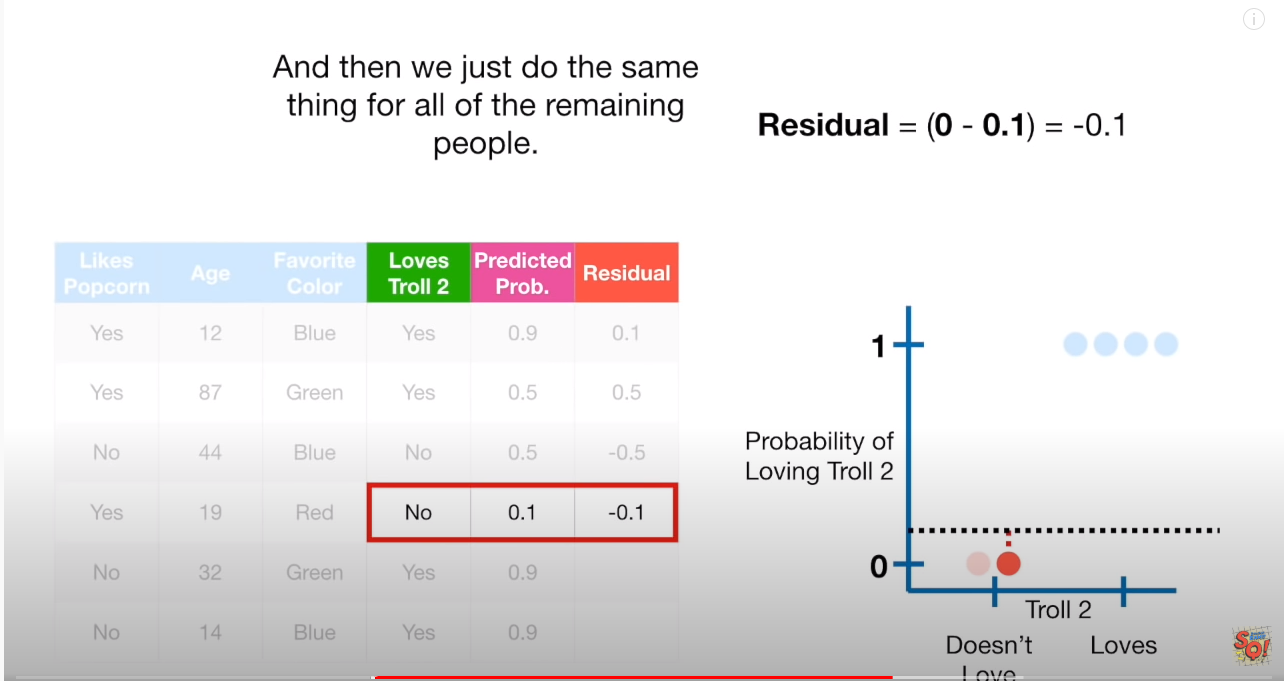
하기 그림을 통해보면, classfication 문제이기 때문에, y축은 0,1 로 구성되어 있다.
- y=1 : 파란점. YES
- y=0 : 빨간점. NO
- 점선 : 초기값이 0.7 인 확률
오차를 구하면 하기와 같다. 각 실데이터 6개를 차례로 구하며,
파란점 : (1-0.7)=0.3, (1-0.7)=0.3, (1-0.7)=0.3, (1-0.7)=0.3
빨강점 : (0-0.7)=-0.7, (0-0.7)=-0.7
“initial Predict = 초기 예측값” 으로 첫 Residual 을 구했다면, 이를 Target으로 분류하는 (Residual을 분류하는) Tree01 을 만든다.
당연히, Gini Impurity 나 Entropy 를 이용하여, Infomation Gain 이론에 따라, Tree 작업을 한다.
3. Tree01 를 통한 실제 data의 예측값 구하기 (1번째 GBTC 예측값이 되겠다.)
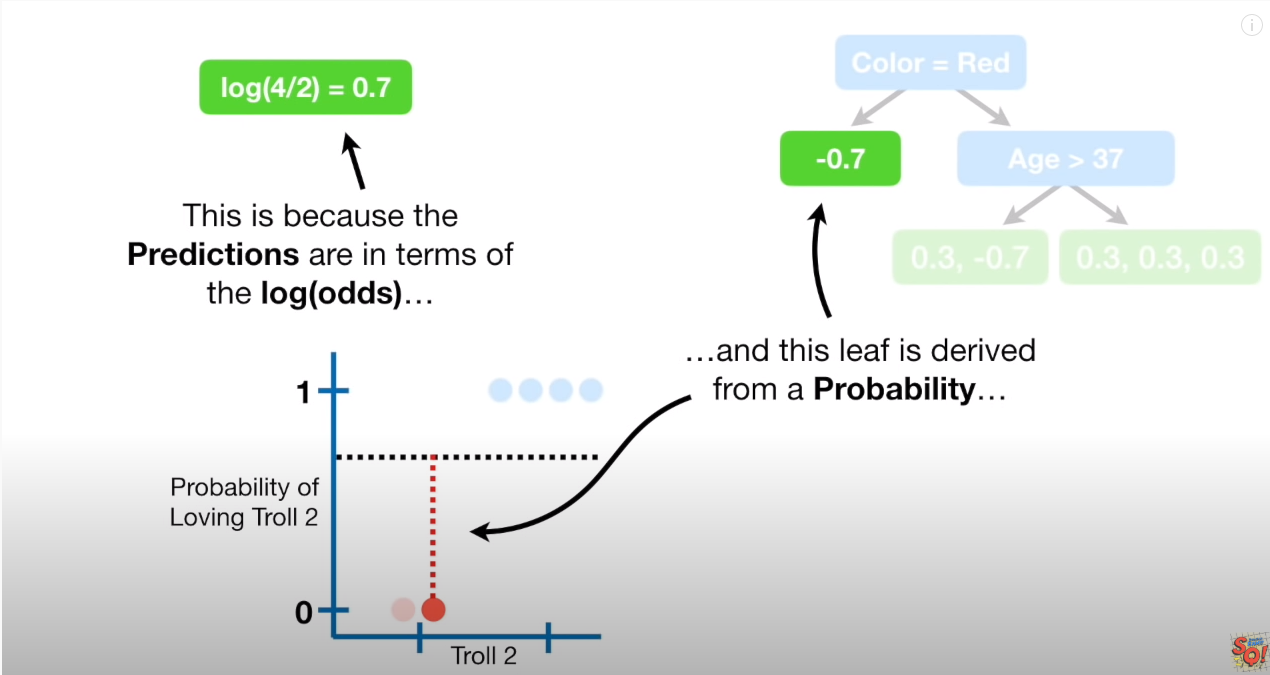
다만, Regression 과 다른 주의점이 있는데 바로 Tree 들의 예측값 이다.
학습을 했다면, 이제 1번째 예측값 (0번째 예측값은 initial predict인 0.7)을 만들고, learnin rate 곱하는 등 Gradient Boosting을 향해 나아가야 하는데
생각해보면, Residual 값을 그대로 사용한다면, 확률값 끼리에 대한 +- 연산을 직접하는 것이 된다.
위 그림에서 보면, 만약 GBTR과 같은 과정이라면,
0.7 + (learning rate * -0.7) 일텐데 확률이란 개념은 더하기, 빼기 연산의 개념이 아니다. 더욱이 initial predict 값은 Log(odds)를 통해 확률로 구현되었음을 기억하자
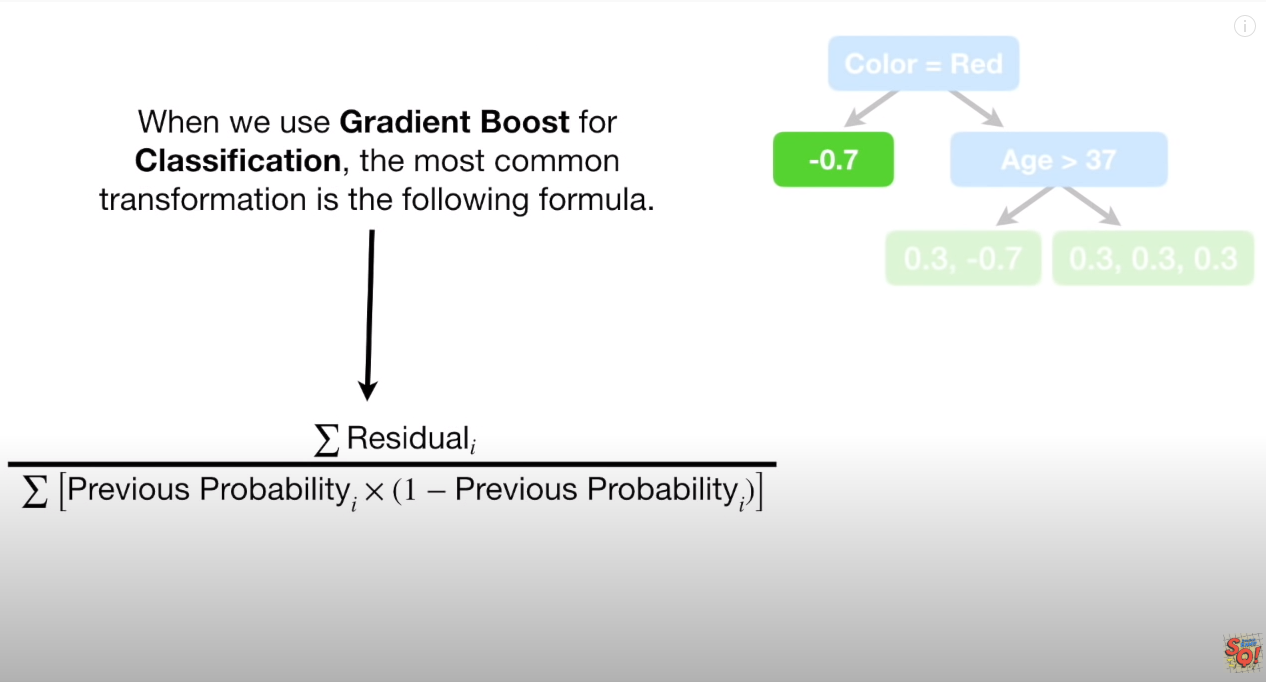
따라서, 예측값을 위해 현재의 Redidual (위 그림에서는 -0.7) 값을 다르게 표현해줘야 하는데 아래 식이 그 공식이다.
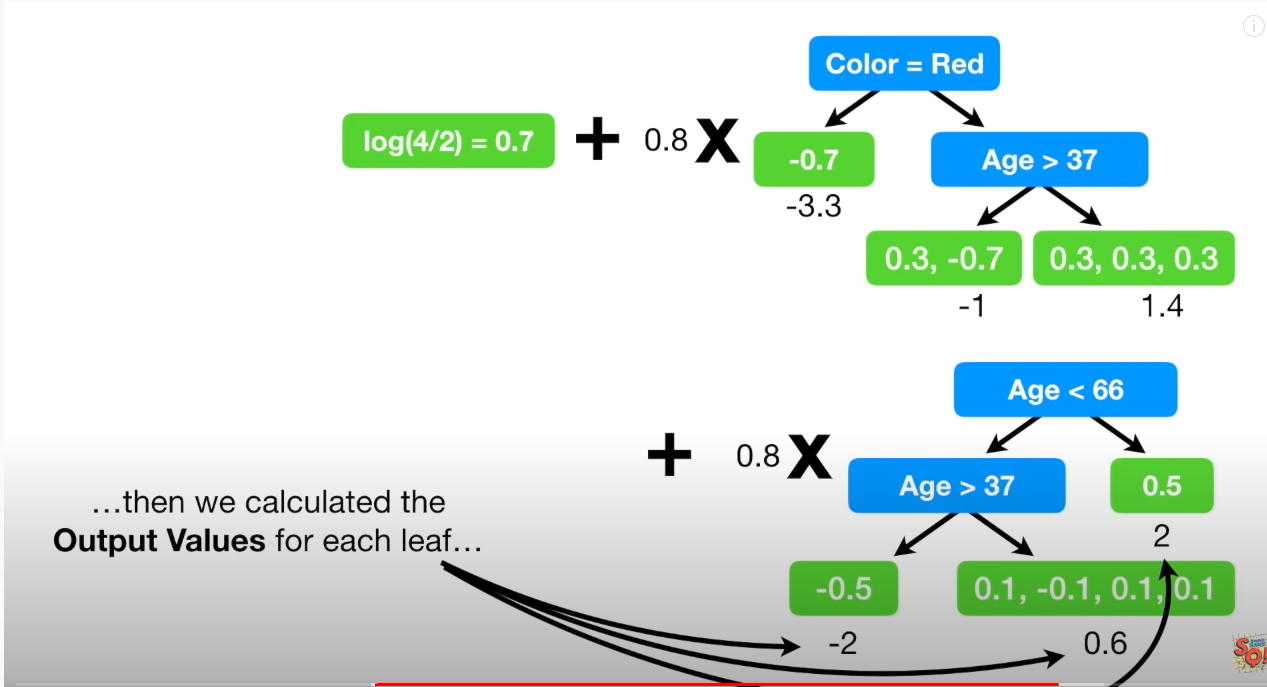
위 식을 거치면 -0.7 => -3.3 으로 변환이 된다.
나머지 값 역시 보면, [0.3,-0.7] => (0.3 + -0.7)/( (0.7(1-0.7)+(0.7(1-0.7) ) => -1 등이 된다.
이를 여기서는 Log(odds) 값으로 변환해는 컨셉이라고 이해하자.
새로운 Log(odds)는 하기 같이 실제 data를 Tree01를 통해 대입하면, learning rate로 scaled 되어서, 1.8 이란 숫자가 나오게 된다. (하기그림)
여기서 1.8 도출이 끝나는게 아니라, 다시 확률값으로 변환시켜줘야 하는 점이 중요하다.!!
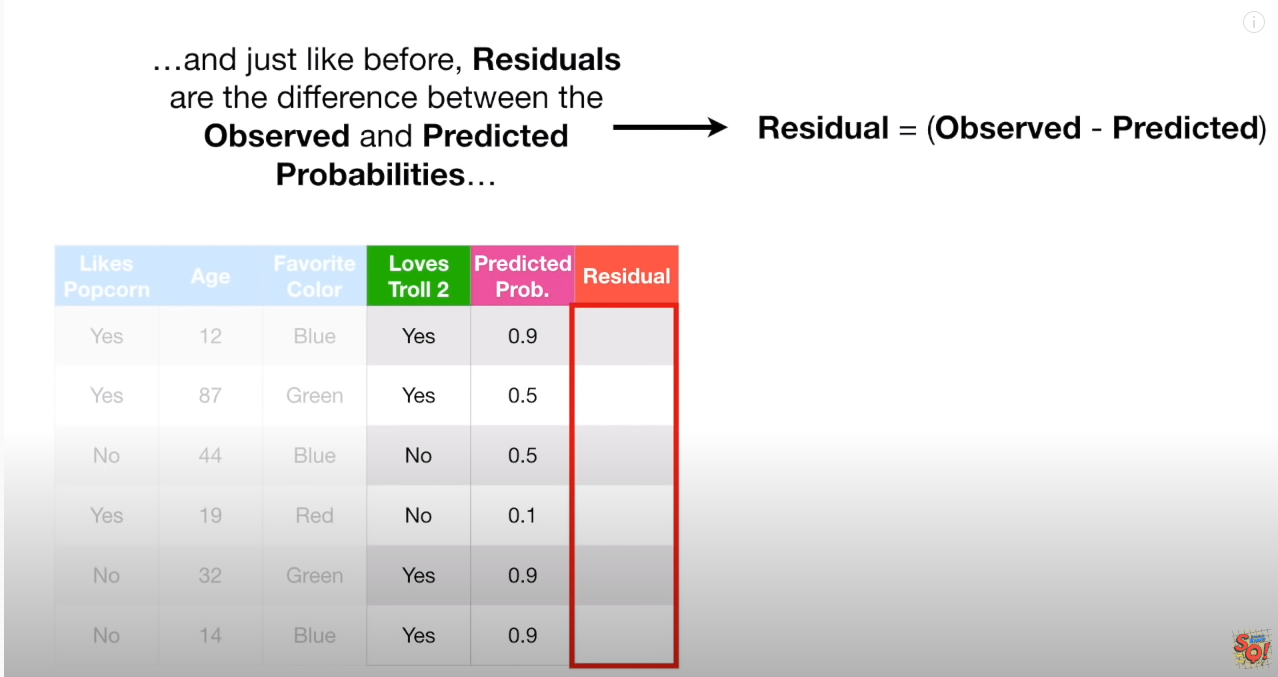
예측값을 확률값으로 변환해주기!!
위에서 언급된 logit function p = e^1.8 / (1+e^1.8) 를 통해 구하면 0.9 가 된다.
나머지 5개 샘플들도, Tree01 을 통해서 예측값 산출 -> 확률값으로 변환 해주면, 아래와 같은 값(Tree01 을 통해 새로 얻은 확률값)을 얻게 되고, 이를 바탕으로 다시 Tree02 를 위한 Residual를 구한다.
4. 오차를 이용한 2번째 Tree 만들기
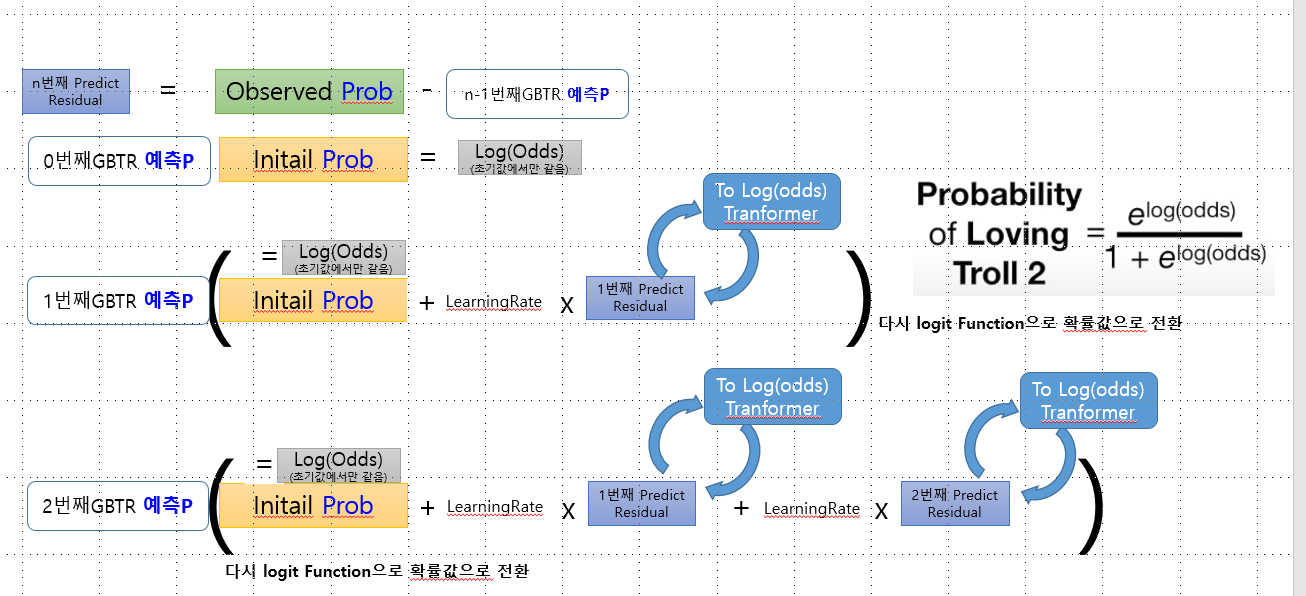
여기서부터는 다시 2번,3번으로 돌아가서 반복이 된다. 따라서 최종적인 모습은 다음과 같다.
요약
- 초기 Initial leaf 값은 확률값이며, 이는 Log(odds) 로 해석이 가능한다
- Residual를 학습시켜서 Tree를 만들때, Residual 들은 확률간의 +- 개념이 불가능하기에 별도의 output value 로 전환이 필요하다.(
새로운 Log(odds)값이라고 일컫기도 한다) - 실제 변경된 확률예측값을 구할때는 learning rate를 반영한
새로운 Log(odds)를 다시 확률값으로 변경해줘야 한다.




Comments